question_answer 16)

Number of persons in various age groups in a town is given in the following table

Age group	Number of persons
1-14	2 lakh
15-29	1 lakh 60 thousands
30-40	1 lakh 20 thousands
45-59	1 lakh 20 thousands
60-74	80 thousands
75 and above	40 thousands

Draw a bar graph to represent the above information and answer the following questions, (take 1 unit length = 20 thousands) (a) Which two age groups have same population? (b) All persons in the age group of 60 and above are called senior citizens. How many senior citizens are there in the town?

Answer:

To draw the bar graph, we will use the following steps. Firstly, draw two perpendicular lines, one is horizontal and one is vertical. Along the horizontal line mark 'age-group' and along vertical line mark 'number of persons'. (ii) Now, take scale of 1 unit length = 20000 along the vertical line and then mark the corresponding values. Also, the heights of bars for various groups are as follows:

1-14	\[\frac{200000}{20000}=10\text{units}\]
15-29	\[\frac{160000}{20000}=8\text{units}\]
30-44	\[\frac{120000}{20000}=6\text{units}\]
45-59	\[\frac{120000}{20000}=6\text{units}\]
60-74	\[\frac{80000}{20000}=4\text{units}\]
75 and above	\[\frac{40000}{20000}=2\text{units}\]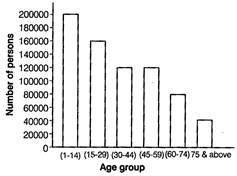

(iii) Draw bar of equal width and of height calculated in Step (ii) on the horizontal line with equal gap between them. Thus, we get the following bar graph (a) From bar graph, we see that the lengths of bars for age group 30-44 and 45-59 are same, so age group (30-44) and (45-559) have the same population. (b) \[\because \] persons having age 60 or above are called senior citizens. \[\therefore \] Number of senior citizens in the town = Number of persons of age group (60-74) + Number of persons of age 75 and above = 80000 + 40000 = 120000