question_answer 65)

                  A simple pendulum of time period 1s and length \[l\] is hung from a fixed support at O, such that the bob is at a distance H vertically above A on the ground Fig. The amplitude is \[{{\theta }_{0}}\]. The string snaps at \[\theta ={{\theta }_{0}}/2\]. Find the time taken by the bob to bit die ground. Also find distance from A where bob hits the ground. Assume \[{{\theta }_{0}}\] to be small so that \[\sin \,{{\theta }_{0}}\,;\,{{\theta }_{0}}\] and \[\cos \,{{\theta }_{0}}\,;\,1\].

Answer:

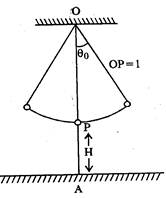
                  Here, angular amplitude \[={{\theta }_{0}}\]. Then die angular displacement of the pendulum at any instant is given by                 \[\theta =\,{{\theta }_{0}}\,\sin \,\omega t=\,\theta {{ & }_{0}}\,\sin \frac{2\pi }{T}t\]                 Since \[T=1\,s\]                 \[\therefore \] \[\theta =\,{{\theta }_{0}}\,\sin \,2\pi t\]                          ?. (i)                 Let at time \[{{t}_{1}},\,\,\theta ={{\theta }_{2}}/2\]                 \[\therefore \] \[\frac{1}{2}\,=\,\sin 2\,\pi \,{{t}_{1}}\] or \[3\pi \,{{t}_{1}}\,=\,\frac{\pi }{6}\]                 or \[{{t}_{1}}=\,\frac{1}{12}\,s.\]                 Differentiating eqn.(i) w.r.t. t, we get                 \[\frac{d\theta }{dt}=2\pi \,{{\theta }_{0}}\,\cos 2\pi \,t\]                 When \[t\,=\,{{t}_{1}}=\,\frac{1}{12}\]                 \[\therefore \] \[\frac{d\theta }{dt}=2\pi \,{{\theta }_{0}}\,\cos \frac{2\pi }{12}\,=2\pi {{\theta }_{0}}\,\times \frac{\sqrt{3}}{2}\]                 \[=\,\sqrt{3}\,\pi \,{{\theta }_{0}}\]                 This is the angular velocity of the pendulum.                 Now \[\upsilon \,=\,\omega r\]                 \[\therefore \] \[\upsilon =\,\sqrt{3}\,\pi \,{{\theta }_{0}}\,l\]                 \[(\because \,r=\,l)\]                 The vertical component of velocity of the bob                 \[{{u}_{y}}\,=\,\upsilon \,\sin \,{{\theta }_{0}}\,=\,\sqrt{3}\,\pi \,{{\theta }_{0}}\,l\,\sin \,{{\theta }_{0}}\]                 and horizontal component of velocity, \[{{u}_{x}}\]                 \[=\sqrt{3}\,\,\pi \,{{\theta }_{0}}\,l\,\cos {{\theta }_{0}}\]                 The height of the bob, when the pendulum snaps,                 \[H'\,=H+l-l\,\cos \frac{{{\theta }_{0}}}{2}\]                 \[=\,H+l\,\left( 1-\cos \frac{{{\theta }_{0}}}{2} \right)\]                 Let \[t\] be the time taken by the bob to fall through height \[H'\].                 Using \[h=ut+\,\frac{1}{2}\,g{{t}^{2}},\] we get                 \[H'\,=\,\left( \sqrt{3}\,\pi {{\theta }_{0}}\,l\,\sin {{\theta }_{0}} \right)\,t\,+\frac{1}{2}\,g{{t}^{2}}\]                 or \[{{t}^{2}}+\,\left( \frac{2\sqrt{3}\,\pi \,{{\theta }_{0}}\,l\,\sin \,{{\theta }_{0}}}{g} \right)\,t-\,\frac{2H'}{g}\,=0\]                 \[\therefore \] \[t\,=\,\frac{\left( \frac{-2\sqrt{3}\,\pi \,{{\theta }_{0}}\,l\,\sin {{\theta }_{0}}}{g} \right)\ \pm \,\sqrt{\frac{12{{\pi }^{2}}\theta _{0}^{2}{{l}^{2}}\,{{\sin }^{2}}\,{{\theta }_{0}}\,}{{{g}^{2}}}+\,\frac{8H'}{g}}}{2}\]\[=\,\frac{-2\sqrt{3}\,\pi \,{{\theta }_{0}}\,l\,\sin \,{{\theta }_{0}}\,\pm \,\sqrt{12\,{{\pi }^{2}}\,\theta _{0}^{2}\,{{l}^{2}}\,{{\sin }^{2}}\,{{\theta }_{0}}+\,8gH'}}{2g}\]                 Since \[{{\theta }_{0}}\] is very small, so \[\sin \,{{\theta }_{0}}={{\theta }_{0}}\] and \[{{\sin }^{2}}{{\theta }_{0}}\simeq 0\]  (negligible)                 Hence \[t=\,\frac{-2\,\sqrt{3}\,\pi \,l\,\theta _{0}^{2}\,\pm \,\sqrt{8\,g\,H'}}{2g}\]                 Neglecting a term containing \[\theta _{0}^{2}\]                 \[\therefore \] \[t=\,\sqrt{\frac{2\,H'}{g}}\]                                ?.. (ii)                 Since \[H'=H+l\left( 1-\cos \frac{{{\theta }_{0}}}{2} \right)\]                 \[\therefore \] for small \[{{\theta }_{0}},\,\,\cos \,\,\frac{{{\theta }_{0}}}{2}=1\]                 Hence \[H'=H\]                 \[\therefore \] from eqn. (ii), \[t=\,\sqrt{\frac{2H}{g}}\]               ?.. (iii)                 The horizontal distance travelled by the bob of pendulum in time \[t=\sqrt{\frac{2H}{g}}\,\] is given by                 \[x=\,({{\mu }_{x}})t=\,\sqrt{3}\,\pi {{\theta }_{0}}\,l\,\sin \,{{\theta }_{0}}\,\times \sqrt{\frac{2H}{g}}\]                 \[=\sqrt{3}\,\pi \,l\,\theta _{0}^{2}\,\times \sqrt{\frac{2H}{g}}\]               \[\,\left( \because \,\,\sin \,{{\theta }_{0}}\,=\,{{\theta }_{0}} \right)\]