Trigonometrical Ratios or Functions
Category : JEE Main & Advanced
In the right angled triangle \[OMP,\] we have base \[=OM=x,\] perpendicular \[=PM=y\] and hypotenuse \[=OP=r\]. We define the following trigonometric ratio which are also known as trigonometric function.
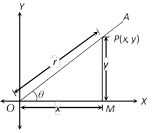
\[\sin \theta =\frac{\text{Perpendicular}}{\text{Hypotenues}}=\frac{y}{r}\]
\[\frac{2n\pi \pm A}{2}\]
\[\tan \theta =\frac{\text{Perpendicular}}{\text{Base}}=\frac{y}{x}\]
\[\cot \theta =\frac{\text{Base}}{\text{Perpendicular}}=\frac{x}{y}\]
\[\sec \theta =\frac{\text{Hypotenues}}{\text{Base}}=\frac{r}{x}\]
\[\text{cosec}\theta =\frac{\text{Hypotenues}}{\text{Perpendicular}}=\frac{r}{y}\]
(1) Relation between trigonometric ratios (functions)
(i) \[\frac{\sqrt{4-\sqrt{2}-\sqrt{6}}}{2\sqrt{2}}\]
(ii) \[\tan \theta .\cot \theta =1\]
(iii) \[\cos \theta .\sec \theta =1\]
(iv) \[\tan \frac{A}{2}\] (v) \[\cot \theta =\frac{\cos \theta }{\sin \theta }\]
(2) Fundamental trigonometric identities
(i) \[{{\sin }^{2}}\theta +{{\cos }^{2}}\theta =1\]
(ii) \[1+{{\tan }^{2}}\theta ={{\sec }^{2}}\theta \]
(iii) \[1+{{\cot }^{2}}\theta =\text{cose}{{\text{c}}^{2}}\theta \]
(3) Sign of trigonometrical ratios or functions : Their signs depends on the quadrant in which the terminal side of the angle lies.
In brief: A crude aid to memorise the signs of trigonometrical ratio in different quadrant. "Add Sugar To Coffee".
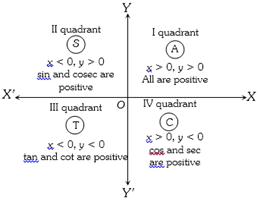
Algorithm : First determine the sign of the trigonometric function.
If \[\theta \] is measured from\[{X}'OX\] i.e., {(p ± q, 2p – q)} then retain the original name of the function.
If \[\theta \] is measured from \[{Y}'OY\] i.e.,\[\left\{ \frac{\pi }{2}\pm \theta ,\,\frac{3\pi }{2}\pm \theta \right\}\], then change sine to cosine, cosine to sine, tangent to cotangent, cot to tan, sec to cosec and cosec to sec.
(4) Variations in values of trigonometric functions in different quadrants : Let \[X'OX\] and \[YOY'\] be the coordinate axes. Draw a circle with centre at origin O and radius unity.
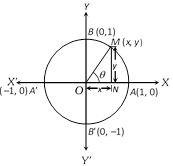
Let \[M(x,y)\] be a point on the circle such that \[\angle AOM=\theta \] then \[x=\cos \theta \] and \[y=\sin \theta \]; \[-1\le \cos \theta \le \]1 and \[-1\le \sin \theta \le 1\] for all values of \[\theta \].
| II-Quadrant (S) | I-Quadrant (A) |
| \[\sin \theta \to \] decreases from 1 to 0 | \[\sin \theta \to \] increases from 0 to 1 |
| \[\cos \theta \to \] decreases from 0 to - 1 | \[\cos \theta \to \] decreases from 1 to 0 |
| \[\tan \theta \to \] increases from \[-\,\infty \] to 0 | \[\tan \theta \to \]increases from 0 to \[\infty \] |
| \[\cot \theta \to \] decreases from 0 to \[-\,\,\infty \] | \[\cot \theta \to \] decreases from \[\infty \] to 0 |
| \[\sec \theta \to \] increases from \[-\,\,\infty \] to - 1 | \[\sec \theta \to \]increases from 1 to \[\infty \] |
| \[\text{cosec}\theta \to \] increases from 1 to \[\infty \] | \[\text{cosec}\theta \to \] decreases from \[\infty \] to 1 |
| III-Quadrant (T) | IV-Quadrant (C) |
| \[\sin \theta \to \] decreases from 0 to - 1 | \[\sin \theta \to \] increases from - 1 to 0 |
| \[\cos \theta \to \] increases from - 1 to 0 | \[\cos \theta \to \] increases from 0 to 1 |
| \[\tan \theta \to \] increases from 0 to \[\infty \] | \[\tan \theta \to \] increases from \[-\,\infty \] to 0 |
| \[\cot \theta \to \] decreases from \[\infty \] to 0 | \[\cot \theta \to \]decreases from 0 to \[-\,\infty \] |
| \[\sec \theta \to \] decreases from - 1 to \[-\,\infty \] | \[\sec \theta \to \] decreases from \[\infty \] to 1 |
| cosecq ® increases from \[-\,\infty \] to - 1 | cosecq ® decreases from - 1 to \[-\,\infty \] |
You need to login to perform this action.
You will be redirected in
3 sec
