Solutions of Triangles
Category : JEE Main & Advanced
Different formulae will be used in different cases and sometimes the same problem may be solved in different ways by different formulae. We should, therefore, look for that formula which will suit the problem best.
(1) Solution of a right angled triangle
(2) Solution of a triangle in general
(1) Solution of a right angled triangle
(i) When two sides are given: Let the triangle be right angled at C. Then we can determine the remaining elements as given in the following table.
| Given | Required |
| \[a,b\] | \[\tan A=\frac{a}{b},\,B={{90}^{o}}-A,\,\,c=\frac{a}{\sin A}\] |
| \[a,c\] | \[\sin A=\frac{a}{c},\,\,b=c\cos A,B={{90}^{o}}-A\] |
(ii) When a side and an acute angle are given : In this case, we can determine the remaining elements as given in the following table
| Given | Required |
| \[a,A\] | \[B={{90}^{o}}-A,\,b=a\cot A,\,c=\frac{a}{\sin A}\] |
| \[c,A\] | \[B={{90}^{o}}-A,\,\,a=\,c\,\sin ,\,\,A,\,b=c\,\cos A\] |
(2) Solution of a triangle in general
(i) When three sides a, b and c are given : In this case, the remaining elements are determined by using the following formulae, \[\Delta =\sqrt{s(s-a)(s-b)(s-c)}\], where \[2s=a+b+c\]= perimeter of triangle
\[\sin A=\frac{2\Delta }{bc},\,\,\sin B=\frac{2\Delta }{ac},\,\,\sin C=\frac{2\Delta }{ab}\]
\[\tan \frac{A}{2}=\frac{\Delta }{s(s-a)},\,\,\tan \frac{B}{2}=\frac{\Delta }{s(s-b)},\,\,\tan \frac{C}{2}=\frac{\Delta }{s(s-c)}\].
(ii) When two sides a, b and the included angle C are given: In this case, we use the following formulae \[\Delta =\frac{1}{2}ab\sin C;\]\[\tan \frac{A-B}{2}=\frac{a-b}{a+b}\cot \frac{C}{2};\] \[\frac{A+B}{2}={{90}^{o}}-\frac{C}{2}\] and \[c=\frac{a\sin C}{\sin A}\].
(iii) When one sides a and two angles A and B are given : In this case, we use the following formulae to determine the remaining elements \[A+B+C={{180}^{o}}\]
\[\Rightarrow \] \[C={{180}^{o}}-A-B\]
\[b=\frac{a\sin B}{\sin A}\,\text{and }c=\frac{a\sin C}{\sin A}\] \[\Rightarrow \] \[\Delta =\frac{1}{2}ca\sin B\].
(iv) When two sides a, b and the angle A opposite to one side is given : In this case, we use the following formulae
\[\sin B=\frac{b}{a}\sin A\] .....(i)
\[C={{180}^{o}}-(A+B),\,c=\frac{a\sin C}{\sin A}\].
Special Cases
Case I : When A is an acute angle
(a) If \[a<b\sin A,\] there is no triangle. When \[a<b\sin A,\] then (i), \[\sin B>1,\]which is impossible.
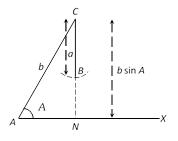
(b) If \[a=b\sin A,\] then only one triangle is possible which is right angled at B. When \[a=b\sin A,\] then from sine rule. \[\sin B=1,\] \[\therefore \] \[\angle B={{90}^{o}}\] from fig. It is clear that \[CB=a=b\sin A\]
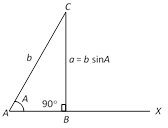
Thus, in this case, only one triangle is possible which is right angled at B.
(c) If \[a>b\sin A,\] then three possibilities will arise:
(i) \[a=b\] In this case, from sine rule \[\sin B=\sin A\]
\[\therefore \,\,B=A\] or \[B={{180}^{o}}-A\].
But \[B={{180}^{o}}-A\] Þ \[A+B={{180}^{o}}\], which is not possible in a triangle. \[\therefore \] In this case, we get \[\angle A=\angle B\].
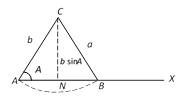
Hence, if \[b=a>b\sin A\] then only one isosceles triangle ABC is possible in which \[\angle A=\angle B\]. (ii) \[a>b\] In the following figure, Let \[AC=b,\,\angle CAX=A,\] and \[a>b,\] also \[a>b\sin A\].
Now taking C as centre, if we draw an arc of radius a, it will intersect AX at one point B and hence only one \[\Delta ABC\] is constructed. Also this arc will intersect XA produced at \[{B}'\] and \[\Delta A{B}'C\] is also formed but this \[\Delta \] is inadmissible (because \[\angle CA{B}'\] is an obtuse angle in this triangle)
Hence, if \[a>b\] and \[a>b\sin A,\]then only one triangle is possible.
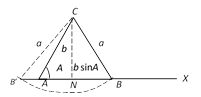
(iii) \[b>a\] (i.e., \[b>a>b\sin A)\]
In fig. let \[AC=b,\,\angle CAX=A\]. Now taking C as centre, if we draw an arc of radius a, then it will intersect AX at two points \[{{B}_{1}}\] and \[{{B}_{2}}\]. Hence if \[b>a>\sin A,\] then there are two triangles.

Case II : When A is an obtuse angle: In this case, there is only one triangle, if \[a>b\]

Case III: \[b>c\] and \[B={{90}^{o}}\] Again the circle with A as centre and b as radius will cut the line only in one point. So, only one triangle is possible.
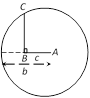
Case IV: \[b\le c\] and \[B={{90}^{o}}\] The circle with A as centre and b as radius will not cut the line in any point. So, no triangle is possible. This is, sometimes called an ambiguous case. Alternative method: By applying cosine rule, we have \[\cos B=\frac{{{a}^{2}}+{{c}^{2}}-{{b}^{2}}}{2ac}\]
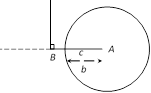
\[\Rightarrow \]\[{{a}^{2}}-(2c\cos B)a+({{c}^{2}}-{{b}^{2}})=0\]
\[\Rightarrow \] \[a=c\cos B\pm \sqrt{{{(c\cos B)}^{2}}-({{c}^{2}}-{{b}^{2}})}\]
\[\Rightarrow \] \[a=c\cos B\pm \sqrt{{{b}^{2}}-{{(c\sin B)}^{2}}}\]
This equation leads to following cases:
Case I : If \[b<c\sin B\],no such triangle is possible.
Case II : Let \[b=c\sin B,\] there are further following case.
(a) B is an obtuse angle
\[\Rightarrow \] \[\cos B\] is negative. There exists no such triangle.
(b) B is an acute angle
\[\Rightarrow \] \[\cos B\] is positive. There exists only one such triangle.
Case III : Let \[b>c\sin B\]. There are further following cases :
(a) B is an acute angle \[\Rightarrow \] \[\cos B\] is positive.
In this case two values of a will exists if and only if \[c\cos B>\sqrt{{{b}^{2}}-{{(c\sin B)}^{2}}}\] or \[c>b\] . Two such triangle is possible. If \[c<b,\] only one such triangle is possible.
(b) B is an obtuse angle \[\Rightarrow \] \[\cos B\] is negative. In this case triangle will exist if and only if \[\sqrt{{{b}^{2}}-{{(c\sin B)}^{2}}}>|c\cos B|\] \[\Rightarrow \] \[b>c\]. So, in this case only one such triangle is possible. If \[b<c\] there exists no such triangle.
You need to login to perform this action.
You will be redirected in
3 sec
