Method for Finding Principal Value
Category : JEE Main & Advanced
Suppose we have to find the principal value of \[\theta \] satisfying the equation \[\sin \theta =-\frac{1}{2}\].
Since \[\sin \theta \] is negative, \[\theta \] will be in 3rd or 4th quadrant. We can approach 3rd or 4th quadrant from two directions. If we take anticlockwise direction the numerical value of the angle will be greater than \[\pi \]. If we approach it in clockwise direction the angle will be numerically less than \[\pi \]. For principal value, we have to take numerically smallest angle. So for principal value.
(1) If the angle is in 1st or 2nd quadrant we must select anticlockwise direction and if the angle is in 3rd or 4th quadrant, we must select clockwise direction.
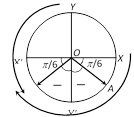
(2) Principal value is never numerically greater than \[\pi \].
(3) Principal value always lies in the first circle (i.e., in first rotation). On the above criteria, \[\theta \] will be \[-\frac{\pi }{6}\] or \[-\frac{5\pi }{6}.\] Between these two \[-\frac{\pi }{6}\] has the least numerical value. Hence \[-\frac{\pi }{6}\] is the principal value of \[\theta \] satisfying the equation \[\sin \theta =-\frac{1}{2}.\]
From the above discussion, the method for finding principal value can be summed up as follows :
(i) First draw a trigonometrical circle and mark the quadrant, in which the angle may lie.
(ii) Select anticlockwise direction for 1st and 2nd quadrants and select clockwise direction for 3rd and 4th quadrants.
(iii) Find the angle in the first rotation.
(iv) Select the numerically least angle. The angle thus found will be principal value.
(v) In case, two angles one with positive sign and the other with negative sign qualify for the numerically least angle, then it is the convention to select the angle with positive sign as principal value.
You need to login to perform this action.
You will be redirected in
3 sec
