Intervals
Category : JEE Main & Advanced
There are four types of interval:
(1) Open interval : Let a and b be two real numbers such that \[a<b\], then the set of all real numbers lying strictly between \[a\] and \[b\] is called an open interval and is denoted by \[[a,\,\,b]\] or \[(a,\,\,b)\]. Thus, \[[a,\,\,b]\] or \[(a,\,\,b)=\{x\in R\,:\,a<x<b\}\].
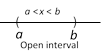
(2) Closed interval : Let a and b be two real numbers such that \[a<b,\] then the set of all real numbers lying between \[a\] and \[b\] including \[a\] and \[b\] is called a closed interval and is denoted by \[[a,\,\,b]\]. Thus, \[[a,\,\,b]=\{x\in R\,:\,a\le x\le b\}\]

(3) Open-Closed interval : It is denoted by \[[a,\,\,b]\] or \[(a,\,\,b]\] and \[[a,\,\,b]\] or \[(a,\,\,b]=\{x\in R\,:\,\,a<x\le b\}\].
![]()
(4) Closed-Open interval : It is denoted by \[[a,\,\,b]\] or \[[a,\,\,b)\] and \[[a,\,\,b]\] or \[[a,\,\,b)=\{x\in R\,:\,\,a\le x<b\}\]
![]()
You need to login to perform this action.
You will be redirected in
3 sec
