Operation of Multiplication on Square Roots
Category : 8th Class
We use the fact that the product of two radicals is the same as the radical of the product and vice versa.
![]()
we have, \[\sqrt{a}\times \sqrt{a}={{a}^{\frac{1}{2}}}\times {{a}^{\frac{1}{2}}}={{a}^{\frac{1}{2}+\frac{1}{2}}}={{a}^{1}}\] \[\therefore \]
\[\sqrt{3}\times \sqrt{3}=3\]
Also, \[\sqrt{3}\times \sqrt{5}=\sqrt{3\times 5}=\sqrt{15}\]
![]() Problems Related to Navigation
Problems Related to Navigation
A ship sails 42 km due east and then 25 km due north. How far is the ship from its starting position when it completes this voyage?
Solution:
Let the distance of the ship from its starting point be x km.
From the figure given below the distance is OP
Thus \[\Delta OPA\] is a right triangle with right angle at A.
Hence, by Pythagoras' Theorem,
\[O{{P}^{2}}=O{{A}^{2}}+A{{P}^{2}}\]
\[\Rightarrow \]\[{{x}^{2}}={{42}^{2}}+{{25}^{2}}\]\[\Rightarrow \]\[{{x}^{2}}=2389\]\[\Rightarrow \] \[x=\sqrt{2389}=48.88\,km\]
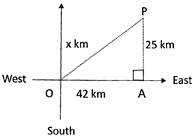
So, the ship is about 48.88 km far from the starting point.
![]()
The length of the diagonal of a rectangular paddock is 61 m and the length of one side is 60 m.
Find:
(a) The width of the paddock.
(b) The length of the fencing needed to enclose the paddock.
Solution:
(a) Let the width of the paddock be X By Pythagoras' Theorem, from the diagram given below.
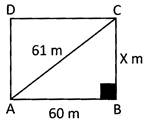
\[{{x}^{2}}={{61}^{2}}-{{60}^{2}}\]
\[{{x}^{2}}=3721-3600\]
\[{{x}^{2}}=121\]
\[x=\sqrt{121}\]
\[x=11\,m\]
So/the width of the paddock is 11 m.
(b) Now, Perimeter \[=\text{2(I}+\text{w)}\]
\[=\text{2(6}0+\text{11)}=\text{2}\times \text{71}=\text{142}\]
So, the length of the fence required to enclose the paddock is 142 m.
![]()
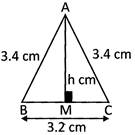
Use the information given in the diagram to find:
(a) Height of the triangle
(b) The area of the triangle
Solution:
(a) By Pythagoras' Theorem in \[\Delta \text{AMC}\],
By symmetry, M is the midpoint of BC;
\[\therefore \] \[MC\frac{1}{2}BC=\frac{3.2}{2}=1.6\,cm\]
\[{{h}^{2}}+{{1.6}^{2}}={{3.4}^{2}}\]
\[{{h}^{2}}+2.56=11.56\]
\[{{h}^{2}}=11.56-2.56\]
\[{{h}^{2}}=9\] \[h=\sqrt{9}=3\]
(b) Area of \[\Delta ABC=\frac{Base\times Height}{2}\]
\[=\frac{3.2\times 3}{2}=4.8\,cm\]
So, the area of \[\Delta \text{ABC is 4}. \text{8 c}{{\text{m}}^{\text{2}}}\]
![]()
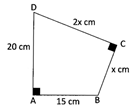
Use the information given in the diagram to find the value of x.
Solution:
Join BD of the quadrilateral to form the right-angled triangles \[\Delta \text{ABD}\] and \[\Delta BCD\].
Let BD = y cm.
By Pythagoras' Theorem in \[\Delta ABD\]
\[{{y}^{2}}={{15}^{2}}+{{20}^{2}}\]
\[=225+400\] \[=625\]
\[\Rightarrow \] \[y=\sqrt{625}=25\]
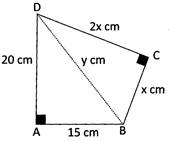
By Pythagoras' Theorem in \[\Delta \,\text{BCD}\]
\[{{x}^{2}}+{{(2x)}^{2}}={{y}^{2}}\]
\[(\because \,y=25)\] \[{{x}^{2}}+4{{x}^{2}}={{25}^{2}}\]
\[5{{x}^{2}}=625\] \[\Rightarrow \] \[\frac{5{{x}^{2}}}{5}=\frac{625}{5}\]
\[{{x}^{2}}=125\] \[\Rightarrow \] \[x=\sqrt{125}\]
\[x=\sqrt{25\times 5}\] \[\Rightarrow \] \[x=5\sqrt{5}\]

![]()

![]() The sum of the numbers \[\text{1}+\text{3}+\text{5}+\text{7}+\text{9}+\]\[\text{11}+\text{13}+\text{15}+\text{17}+\text{19}+\text{21}+\text{23}\] is equal to:
The sum of the numbers \[\text{1}+\text{3}+\text{5}+\text{7}+\text{9}+\]\[\text{11}+\text{13}+\text{15}+\text{17}+\text{19}+\text{21}+\text{23}\] is equal to:
(a) 144
(b) 212
(c) 221
(d) 112
(e) None of these
Answer: (a)
Explanation:
There are 11 odd numbers in the series, therefore, the sum is equal to \[{{11}^{2}}=121\].
![]() The number of odd numbers whose sum results 81 is:
The number of odd numbers whose sum results 81 is:
(a) 5
(b) 6
(c) 8
(d) 9
(e) None of these
Answer: (d)
Explanation:
81 an be written as 1 + 3 + 5 + 7 + 9 + 11 + 13 + 15 + 17.
![]() The Pythagorean triplet whose smallest number is 14 is:
The Pythagorean triplet whose smallest number is 14 is:
(a) 28, 195 & 197
(b) 14, 196 & 198
(c) 14, 197 & 163
(d) 14, 16 & 20
(e) None of these
Answer: (a)
![]() Which one among the following is the perfect square?
Which one among the following is the perfect square?
(a) 130321
(b) 21296
(c) 36501
(d) 27648
(e) None of these
Answer: (a)
![]() The number 16777216 is the square of which one of the following numbers?
The number 16777216 is the square of which one of the following numbers?
(a) 4276
(b) 4096
(c) 4086
(d) 5006
(e) None of these
Answer: (b)
![]() What is the value of \[\sqrt{\text{522756}}\]?
What is the value of \[\sqrt{\text{522756}}\]?
(a) 1232
(b) 2434
(c) 1324
(d) 1426
(e) 1234
Answer: (e)
Explanation:
From the prime factorization of \[\sqrt{1522756}\], we get 1234.
![]() What is the value of \[\sqrt{3018+\sqrt{36+\sqrt{169}}}\]?
What is the value of \[\sqrt{3018+\sqrt{36+\sqrt{169}}}\]?
(a) 55
(b) 25 (c) 35
(d) 65
(e) 45
Answer: (a)
Explanation:
Since, \[\sqrt{3018+\sqrt{36+\sqrt{169}}}=55\]
![]() Find the square root of 15876.
Find the square root of 15876.
(a) 126
(b) 144
(c) 184
(d) 156
(e) None of these
Answer: (a)
Explanation:
| 126 | |
| 1 1 | 15876 1 |
| 22 2 | 58 44 |
| 246 6 | 1476 1476 |
| 252 | 0 |
![]() Find the square root of 17424.
Find the square root of 17424.
(a) 132
(b) 124
(c) 142
(d) 172
(e) None of these
Answer: (a)
![]() Simplify: \[\sqrt{\frac{1183}{2023}}\]
Simplify: \[\sqrt{\frac{1183}{2023}}\]
(a) \[\frac{17}{13}\]
(b) \[\frac{1}{13}\]
(c) \[\frac{13}{17}\]
(d) \[\frac{1}{17}\]
(e) \[7\sqrt{2}\]
Answer: (c)
![]() Simplify: \[\sqrt{3\frac{33}{289}}\]
Simplify: \[\sqrt{3\frac{33}{289}}\]
(a) \[\sqrt{\frac{3}{17}}\]
(b) \[\sqrt{\frac{30}{17}}\]
(c) \[\sqrt{\frac{33}{17}}\]
(d) \[\sqrt{\frac{11}{17}}\]
(e) None of these
Answer: (b)
![]() Simplify: \[\sqrt{10.0489}\]
Simplify: \[\sqrt{10.0489}\]
(a) 3.27
(b) 3.07
(c) \[3.17\]
(d) \[3.47\]
(e) None of these
Answer: (c)
![]() Find the value of \[\sqrt{2\sqrt{2\sqrt{2\sqrt{2\sqrt{5}}}}}\]?
Find the value of \[\sqrt{2\sqrt{2\sqrt{2\sqrt{2\sqrt{5}}}}}\]?
(a) \[{{2}^{\frac{1}{31}}}\]
(b) \[{{2}^{\frac{1}{32}}}\]
(c) \[{{2}^{\frac{31}{32}}}\]
(d) \[{{2}^{\frac{30}{31}}}\]
(e) None of these
Answer: (c)
![]() Simplify the given expression and find the value of the expression \[\sqrt{\frac{0.256\times 0.081\times 4.356}{1.5625\times 0.0121\times 129.6\times 64}}\]
Simplify the given expression and find the value of the expression \[\sqrt{\frac{0.256\times 0.081\times 4.356}{1.5625\times 0.0121\times 129.6\times 64}}\]
(a) 1.096
(b) 0,024
(c) 2.196
(d) 4.096
(e) None of these
Answer: (b)
![]() If \[a=\frac{\sqrt{2}+1}{\sqrt{2}-1}\] and \[b=\frac{\sqrt{2}-1}{\sqrt{2}+1}\] then find the value of \[\frac{{{a}^{2}}+ab+{{b}^{2}}}{{{a}^{2}}-ab+{{b}^{2}}}\]
If \[a=\frac{\sqrt{2}+1}{\sqrt{2}-1}\] and \[b=\frac{\sqrt{2}-1}{\sqrt{2}+1}\] then find the value of \[\frac{{{a}^{2}}+ab+{{b}^{2}}}{{{a}^{2}}-ab+{{b}^{2}}}\]
(a) \[32-4\sqrt{2}\]
(b) \[32+4\sqrt{2}\]
(c) 0
(d) \[\frac{7}{5}\]
(e) None of these
Answer: (d)
![]() Find the value of \[\sqrt{6+\sqrt{6+\sqrt{6+---}}}\]
Find the value of \[\sqrt{6+\sqrt{6+\sqrt{6+---}}}\]
(a) (-3, 2)
(b) (-3, -2)
(c) (3, 2)
(d) (3, -2)
(e) None of these
Answer: (d)
![]() A group of students in a class collects Rs. 9216. The amount contributed by each student is equivalent to the number of students in the class. Find the number of students in the class.
A group of students in a class collects Rs. 9216. The amount contributed by each student is equivalent to the number of students in the class. Find the number of students in the class.
(a) 66
(b) 48
(c) 96
(d) 36
(e) None of these
Answer: (c)
You need to login to perform this action.
You will be redirected in
3 sec
