Angle
Category : 7th Class
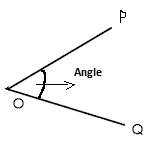
If two rays have common end point then the inclination between two rays is called angle. In the figure O is the vertex, \[\overline{OP}\] and \[\overline{OQ}\] are called arm of the angle. It is represented by notation\[\angle \].
![]() Types of angle
Types of angle
Acute Angle
Tangle whose measure is more than \[0{}^\circ \] and less than \[90{}^\circ .\]
Right Angle
The angle of measure \[90{}^\circ \]
Obtuse Angle
The angle whose measure is more than 90° and less than \[180{}^\circ .\]
Straight Angle
The angle whose measure is \[180{}^\circ \]
Reflex Angle
The angle whose measure is more than \[180{}^\circ \]and less than \[360{}^\circ .\]
Complete Angle
The angle whose measure is 360°.
Equal Angles
Two angles are said to be equal if they are of same measure.
![]() Complementary Angles
Complementary Angles
If the sum of measure of two angles is \[{{90}^{o}}\] then they are said to be complementary angles .e.g \[75{}^\circ \] and \[15{}^\circ \] are complementary angles and they are said to be complement of each other.
![]() Supplementary Angles
Supplementary Angles
If the sum of measure of two angles is \[180{}^\circ \]then they are said to be supplementary angles, e.g \[107{}^\circ \] and \[73{}^\circ \] are said to be supplement of each other.

![]() Which one of the following statements is not true?
Which one of the following statements is not true?
(i) A line segment has finite length
(ii) A line has only one dimension
(iii) A line \[\overleftrightarrow{AB}\] and \[\overleftrightarrow{BA}\]represents the same
(iv) A ray \[\overleftrightarrow{AB}\]and \[\overleftrightarrow{BA}\]represents the same
(a) i, ii
(b) ii and iii
(c) Only iv
(d) iii and iv
(e) None of these
Answer: (c)
Explanation
\[\]and \[\]are different rays. They are started from different end points A and B respectively.
Therefore, option (c) is correct and rest of the options is incorrect.
![]() In the following AD is the bisector of \[\angle EAF\]
In the following AD is the bisector of \[\angle EAF\]
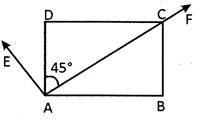
Which one of the following statements is incorrect?
(a) \[\angle EAD\]is an acute angle
(b) \[\angle BAE\]is an obtuse angle
(c)\[\angle FAD\] and \[\angle DAE\]are complement to each other
(d) \[\angle CAD\]and \[\angle DAE\]are not complement to each other
(e) None of these
Answer: (d)
Explanation
Since \[\angle EAD=\angle CAD=45\]degree hence, option (a) is correct.
\[\angle BAE\]is more than 90° therefore, it is obtuse hence, option (b) is also correct.
The sum of \[\angle FAD\]and \[\angle DAE\]is \[90{}^\circ \] hence, option (c) is also correct
\[\left( \angle CADand\text{ }\angle DAE \right)\]and \[\left( \angle FAD\text{ }and\text{ }\angle DAE \right)\]are the same. Therefore, they are also complement.
![]() If the difference of two supplementary angles is \[50{}^\circ \] then find the measurement of the smaller angle.
If the difference of two supplementary angles is \[50{}^\circ \] then find the measurement of the smaller angle.
(a) 67°
(b) \[75{}^\circ \]
(c)\[~65{}^\circ \]
(d) \[90{}^\circ \]
(e) None of these
Answer: (c)
Explanation
Let the one angle be x then other angle will be \[180{}^\circ -x.\]
By given condition\[~x-(180{}^\circ -x)=50{}^\circ \]
\[2x=180{}^\circ +50{}^\circ \Rightarrow 2x=230{}^\circ \text{ }\Rightarrow x=115{}^\circ \]
Hence, the measurement of smaller angle \[=\text{ }180{}^\circ -115{}^\circ =65{}^\circ \]
![]() Find the supplement of an angle which is 8 times of its complement.
Find the supplement of an angle which is 8 times of its complement.
(a) 90°
(b) 100°
(c) 80°
(d) 70°
(e) None of these
Answer: (b)
![]() If the angle and its complement are x and \[\sqrt{x}\] respectively then find the angle.
If the angle and its complement are x and \[\sqrt{x}\] respectively then find the angle.
(a)\[11{}^\circ ,\text{ }12{}^\circ \]
(b) \[13{}^\circ ,\text{ }14{}^\circ \]
(c)\[-15{}^\circ ,1{}^\circ \]
(d) \[81{}^\circ \]
(e) None of these
Answer: (d)
![]() Adjacent Angles
Adjacent Angles
Two angles are said to be adjacent angles, if
In the given figure \[\angle POQ,\text{ }\angle QOR\] are adjacent angles 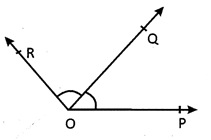
![]() Linear Pair of Angles
Linear Pair of Angles
If the sum of measure of two adjacent angles is \[180{}^\circ \] then they are said to be linear pair of angles. In the linear pair non-common arms are opposite to each other.
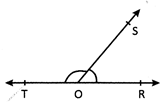
In the figure \[\angle ROS\]and \[\angle TOS\]are linear pairs.
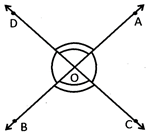
![]() Vertically Opposite Angles
Vertically Opposite Angles
It is the pair of angle which is formed by two intersecting lines having no common arms. In the given figure \[\angle AOC\]and \[\angle BOD\]are vertically opposite angles. Similarly \[\angle AOD\]and \[\angle BOC\]are also vertically opposite angles.
You need to login to perform this action.
You will be redirected in
3 sec
