Operation on the Fractions
Category : 4th Class
![]() Addition of Like Fractions
Addition of Like Fractions
\[\text{Sum of like fractions}=\frac{\text{Sum of numerators}}{\text{common denominator}}\] In addition of like fractions, sum of the numerators will be the numerator for the resulting fraction and the common denominator will be the denominator. \[\frac{P}{R}+\frac{Q}{R}=\frac{P+Q}{R}\]
![]()
Add the following fractions.
Solution: \[\frac{3}{11}+\frac{2}{11}+\frac{5}{11}=\frac{10}{11}\]
![]()
Add the following fractions:
\[\frac{3}{10}+\frac{2}{10}\]
Solution:
\[\frac{3}{10}+\frac{2}{10}=\frac{5}{10}\]
![]() Addition of Unlike Fractions
Addition of Unlike Fractions
Add\[\frac{5}{7}\] and\[\frac{5}{8}\]
Step 1: Convert the fractions into like fractions. \[\frac{5}{7}=\frac{5\times 8}{7\times 8}=\frac{40}{56}\] And \[\frac{5}{8}=\frac{5\times 7}{8\times 7}=\frac{35}{56}\]
Step 2: Add numerator of the fractions\[\text{4}0+\text{35}=\text{75}\].
Step 3: Write the sum as numerator for the required fraction and common denominator as denominator\[\frac{75}{56}\]
![]()
Add\[\frac{12}{19}\]and\[\frac{12}{11}\]
Solution: \[\frac{12}{19}=\frac{12\times 11}{19\times 11}=\frac{132}{209}\]
\[\frac{12}{11}=\frac{12\times 19}{19\times 19}=\frac{228}{209}\]
\[\frac{12}{19}+\frac{12}{11}=\frac{132}{209}+\frac{228}{209},=\frac{132+228}{209}=\frac{360}{209}\]
![]() Subtraction of Like Fractions
Subtraction of Like Fractions
\[\text{Difference of like fractions}=\frac{\text{Difference of numerators}}{\text{Common denominator}}\]
In subtraction of like fractions, the difference of the numerators will be the numerator and the common denominator will be the denominator for the required fraction.
\[\frac{p}{q}-\frac{r}{q}=\frac{p-r}{q}\]
![]()
Solve the following:
\[\frac{5}{7}-\frac{3}{7}\]
Solution: \[\frac{5}{7}-\frac{3}{7}=\frac{5-3}{7}=\frac{2}{7}\]
![]()
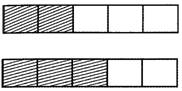
Represent the shaded part in the above figures as a fraction and find their difference.
Solution:
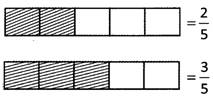
\[\frac{3}{5}-\frac{2}{5}=\frac{3-2}{5}=\frac{1}{5}\]
![]() Subtraction of Unlike
Subtraction of Unlike
Fractions Subtract\[\frac{5}{6}-\frac{4}{5}\]
Step 1: Convert the fractions into like fractions.
\[\frac{5}{6}=\frac{5\times 5}{6\times 5}=\frac{25}{30}\]
\[\frac{4}{5}=\frac{4\times 6}{5\times 6}=\frac{24}{30}\]
Step 2: Find difference of the numerator.
\[\text{25}-\text{24}=\text{1}\].
Step 3: Write the difference as numerator and common denominator as denominator for the required fraction.
\[\frac{1}{30}\]
![]()
Solve\[\frac{7}{9}-\frac{5}{8}\]. Solution:
\[\frac{7}{9}=\frac{7\times 8}{9\times 8}=\frac{56}{72}\]
\[\frac{5}{8}=\frac{5\times 9}{8\times 9}=\frac{45}{72}\]
Now \[\frac{56}{72}-\frac{45}{72}=\frac{56-45}{72}=\frac{9}{72}=\frac{1}{8}\]
You need to login to perform this action.
You will be redirected in
3 sec
