question_answer 1) One drop of soap bubble of diameter D breakes into 27 drops having surface tension T. The change in surface energy is
A)
\[2\pi T{{D}^{2}}\]
done
clear
B)
\[4\pi T{{D}^{2}}\]
done
clear
C)
\[\pi T{{D}^{2}}\]
done
clear
D)
\[8\pi T{{D}^{2}}\]
done
clear
View Answer play_arrow
question_answer 2) The period of a planet around sun is 27 times that of earth. The ratio of radius of planets orbit to the radius of earths orbit is
A)
4
done
clear
B)
9
done
clear
C)
64
done
clear
D)
27
done
clear
View Answer play_arrow
question_answer 3) Three particles each of mass m are kept at vertices of an equilateral triangle of side L. The gravitational field at centre due to these particles is
A)
zero
done
clear
B)
\[\frac{3GM}{{{L}^{2}}}\]
done
clear
C)
\[\frac{9GM}{{{L}^{2}}}\]
done
clear
D)
\[\frac{12}{\sqrt{3}}\frac{GM}{{{L}^{2}}}\]
done
clear
View Answer play_arrow
question_answer 4) In a turbulent flow, the velocity of the liquid in contact with the walls of the tube is
A)
zero
done
clear
B)
maximum
done
clear
C)
in between zero and maximum
done
clear
D)
equal to critical velocity
done
clear
View Answer play_arrow
question_answer 5) A charge q is fixed. Another charge Q is brought near it and rotated in a circle of radius r around it. Work done during rotation is
A)
zero
done
clear
B)
\[\frac{Qq}{4\pi G{{\varepsilon }_{0}}r}\]
done
clear
C)
\[\frac{Qq}{2\pi G{{\varepsilon }_{0}}r}\]
done
clear
D)
None of these
done
clear
View Answer play_arrow
question_answer 6) A diode having potential difference 0.5 V across its junction which does not depend on current, is connected in series with resistance of 20 \[\Omega \] across source. If 0.1 A current passes through resistance then what is the voltage of the source?
A)
1.5V
done
clear
B)
2.0V
done
clear
C)
2.5 V
done
clear
D)
5 V
done
clear
View Answer play_arrow
question_answer 7) Dipole is placed parallel to the electric field. If Q is the work done in rotating the dipole by 60°, then work done in rotating it by 180° is
A)
2W
done
clear
B)
3W
done
clear
C)
4W
done
clear
D)
W/2
done
clear
View Answer play_arrow
question_answer 8) An electron of charge e moves in a circular orbit of radius r around the nucleus at a frequency v. The magnetic moment associated with the orbital motion of the electron is
A)
\[\pi ve{{r}^{2}}\]
done
clear
B)
\[\frac{\pi v{{r}^{2}}}{e}\]
done
clear
C)
\[\frac{\pi v\,e}{r}\]
done
clear
D)
\[\frac{\pi v{{r}^{2}}}{v}\]
done
clear
View Answer play_arrow
question_answer 9) A and B are two identical spherical charged bodies which repel each other with force F, kept at a finite distance. A third uncharged sphere of the same size is brought in contact with sphere B and removed. It is then kept at mid-point of A and B. Find the magnitude of force on C.
A)
F/2
done
clear
B)
F/8
done
clear
C)
F
done
clear
D)
Zero
done
clear
View Answer play_arrow
question_answer 10) A wave equation is \[y=0.1\sin [100\pi t-kx]\]and wave velocity is 100 m/s, its wave number is equal to
A)
\[1{{m}^{-1}}\]
done
clear
B)
\[2{{m}^{-1}}\]
done
clear
C)
\[\pi {{m}^{-1}}\]
done
clear
D)
\[2\pi {{m}^{-1}}\]
done
clear
View Answer play_arrow
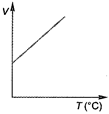
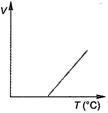
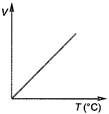
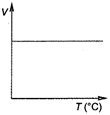
question_answer 11) Volume-temperature graph at atmospheric pressure for a monoatomic gas \[\left( V\text{ }in\text{ }{{m}^{3}},\text{ }T\text{ }in\text{ }{}^\circ C \right)\] is
A)
done
clear
B)
done
clear
C)
done
clear
D)
done
clear
View Answer play_arrow
question_answer 12) An optically active compound
A)
rotates the plane polarized light
done
clear
B)
changing the direction of polarized light
done
clear
C)
do not allow plane polarized light to pass through
done
clear
D)
None of the above
done
clear
View Answer play_arrow
question_answer 13) Power applied to a particle varies with time as \[P=(3{{t}^{2}}-2t+1)\] W, where t is in second. Find the change in its kinetic energy between t = 1 s and t = 4 s.
A)
32 J
done
clear
B)
46 J
done
clear
C)
61 J
done
clear
D)
102 J
done
clear
View Answer play_arrow
question_answer 14) A hockey player receives a corner shot at a speed of 15 m/s at an angle of 30° with the y-axis and then shoots the ball of mass 100 g along the negative x-axis with a speed of 30 m/s. If it remains in contact with the hockey stick for 0.01 s, the force imparted to the ball in the x-direction is
A)
281.25 N
done
clear
B)
187.5N
done
clear
C)
562.5 N
done
clear
D)
375 N
done
clear
View Answer play_arrow
question_answer 15) Two equal charges are separated by a distance d. A third charge placed on a perpendicular bisector at x distance from centre will experience maximum coulomb force, when
A)
\[x=d/\sqrt{2}\]
done
clear
B)
\[x=d/2\]
done
clear
C)
\[x=d/2\sqrt{2}\]
done
clear
D)
\[x=d/2\sqrt{3}\]
done
clear
View Answer play_arrow
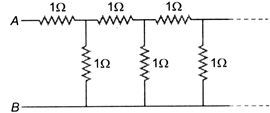
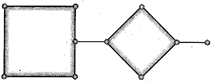
question_answer 16)
The equivalent resistance between points A and B of an infinite network of resistance s each of \[1\,\Omega ,\] connected as shown, is
A)
infinite
done
clear
B)
2\[\Omega \]
done
clear
C)
\[\frac{1+\sqrt{5}}{2}\Omega \]
done
clear
D)
zero
done
clear
View Answer play_arrow
question_answer 17) A circular current carrying coil has a radius R The distance from the centre of the coil off the axis of the coil, where the magnetic induction is I/8th of its value at the centre of the coil is
A)
\[\sqrt{3}R\]
done
clear
B)
\[R/\sqrt{3}\]
done
clear
C)
\[\left( \frac{2}{\sqrt{3}} \right)R\]
done
clear
D)
\[\frac{R}{2\sqrt{3}}\]
done
clear
View Answer play_arrow
question_answer 18) A point source of light is placed 4m below he surface of water of refractive index 5/ 3. The minimum diameter of a disc, which should be placed over the source, on the surface of water to cut-off all light coming out of water is
A)
infinite
done
clear
B)
6 m
done
clear
C)
4m
done
clear
D)
3m
done
clear
View Answer play_arrow
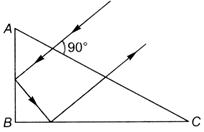
question_answer 19)
A ray falls on a prism ABC (AB =BC) and travels as shown in figure. The minimum refractive index of the prism material should be
A)
\[\frac{4}{3}\]
done
clear
B)
\[\sqrt{2}\]
done
clear
C)
1.5
done
clear
D)
\[\sqrt{3}\]
done
clear
View Answer play_arrow
question_answer 20) The plane face of a planoconvex lens is silvered. If u be the refractive index and R, the radius of curvature of curved surface, then the system will behave like a concave mirror of radius of curvature
A)
\[\mu R\]
done
clear
B)
\[\frac{R}{(\mu -1)}\]
done
clear
C)
\[\frac{{{R}^{2}}}{\mu }\]
done
clear
D)
\[\left[ \frac{(\mu +1)}{(\mu -1)} \right]R\]
done
clear
View Answer play_arrow
question_answer 21)
Two similar accumulators each of emf E and internal resistance r are connected as shown in the following figure. Then, the potential difference between x and y is
A)
2E
done
clear
B)
E
done
clear
C)
zero
done
clear
D)
None of these
done
clear
View Answer play_arrow
question_answer 22) A conducting circular loop is placed in a uniform magnetic field of induction B tesla with its plane normal to the field. Now, the radius of the loop starts shrinking at the rate\[\left( \frac{dr}{dt} \right)\]. Then, the induced emf at the instant when the radius is r, is
A)
\[\pi rB\left( \frac{dr}{dt} \right)\]
done
clear
B)
\[2\pi rB\left( \frac{dr}{dt} \right)\]
done
clear
C)
\[\pi {{r}^{2}}\left( \frac{dr}{dt} \right)\]
done
clear
D)
\[{{\left( \frac{\pi {{r}^{2}}}{2} \right)}^{2}}B\left( \frac{dr}{dt} \right)\]
done
clear
View Answer play_arrow
question_answer 23) The first excitation potential of a given atom is 10.2V. Then, ionization potential must be
A)
20.4V
done
clear
B)
13.6V
done
clear
C)
30.6V
done
clear
D)
40.8V
done
clear
View Answer play_arrow
question_answer 24) A train is approaching with velocity 25 m/s towards a pedestrian standing on the track, frequency of horn of train is 1 kHz. Frequency heard by the pedestrain is (v= 350 m/s)
A)
1077 Hz
done
clear
B)
1167 Hz
done
clear
C)
985 Hz
done
clear
D)
954 Hz
done
clear
View Answer play_arrow
question_answer 25) Intensity of wave A is 91, while of wave B is 7. What is maximum and minimum intensity in YDSE?
A)
82\[I\], 80\[I\]
done
clear
B)
8\[I\], 10\[I\]
done
clear
C)
16\[I\], 4\[I\]
done
clear
D)
4\[I\],\[I\]
done
clear
View Answer play_arrow
question_answer 26) What happens inside optical fibre?
A)
Diffraction
done
clear
B)
Polarization
done
clear
C)
Interference
done
clear
D)
Total internal reflection
done
clear
View Answer play_arrow
question_answer 27) A manometer connected to a closed tap reads\[3.5\times {{10}^{5}}\,N/{{m}^{2}}\]. When the valve is opened, the reading of manometer falls to \[3.0\times {{10}^{5}}\,N/{{m}^{2}}\], then velocity of flow of water is
A)
100 m/s
done
clear
B)
10 m/s
done
clear
C)
1m/s
done
clear
D)
\[10\sqrt{10}\]m/s
done
clear
View Answer play_arrow
question_answer 28) Water is moving with a speed of 5.18 \[m{{s}^{-1}}\] through a pipe with a cross-sectional area of 4.20\[c{{m}^{2}}\]. The water gradually descends 9.66 m as the pipe increase in area to 7.60\[c{{m}^{2}}\]. The speed of flow at the lower level is
A)
3.0\[m{{s}^{-1}}\]
done
clear
B)
5.7\[m{{s}^{-1}}\]
done
clear
C)
3.82\[m{{s}^{-1}}\]
done
clear
D)
2.86\[m{{s}^{-1}}\]
done
clear
View Answer play_arrow
question_answer 29) What is de-Broglie wavelength of electron having energy 10 keV?
A)
\[0.12\overset{\text{o}}{\mathop{\text{A}}}\,\]
done
clear
B)
\[1.2\overset{\text{o}}{\mathop{\text{A}}}\,\]
done
clear
C)
\[12.2\,\overset{\text{o}}{\mathop{\text{A}}}\,\]
done
clear
D)
None of these
done
clear
View Answer play_arrow
question_answer 30) Find beat frequency? Motion of two particles is given by \[{{y}_{1}}=0.25\sin (310t)\] \[{{y}_{2}}=0.25\sin (316t)\]
A)
3
done
clear
B)
\[\frac{3}{\pi }\]
done
clear
C)
\[\frac{6}{\pi }\]
done
clear
D)
6
done
clear
View Answer play_arrow
question_answer 31) Half-life of radioactive substance is 3.20 h. What is the time taken for a 75% of substance to be used?
A)
6.38 h
done
clear
B)
12 h
done
clear
C)
4.18 day
done
clear
D)
1.2day
done
clear
View Answer play_arrow
question_answer 32)
A capacitor of capacitance 1 \[\mu F\] is filled with two dielectrics of dielectric constants 4 and 6. What is the new capacitance?
A)
10\[\mu F\]
done
clear
B)
5\[\mu F\]
done
clear
C)
4\[\mu F\]
done
clear
D)
7\[\mu F\]
done
clear
View Answer play_arrow
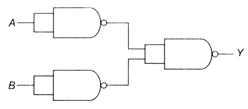
question_answer 33)
The given combination represents the following gate
A)
OR
done
clear
B)
XOR
done
clear
C)
NAND
done
clear
D)
NOR
done
clear
View Answer play_arrow
question_answer 34) In BJT, maximum current flows in which of the following?
A)
Emitter region
done
clear
B)
Base region
done
clear
C)
Collector region
done
clear
D)
Equal in all the regions
done
clear
View Answer play_arrow
question_answer 35) In semiconductors at a room temperature
A)
the valence band is partially empty and the conduction band is partially filled
done
clear
B)
the valence band is completely filled and the conduction band is partially filled
done
clear
C)
the valence band is completely filled
done
clear
D)
the conduction band is completely empty
done
clear
View Answer play_arrow
question_answer 36) If coil is open then L and R become
A)
\[\infty ,0\]
done
clear
B)
\[0,\infty \]
done
clear
C)
\[\infty ,\infty \]
done
clear
D)
0, 0
done
clear
View Answer play_arrow
question_answer 37) In a coil when current changes from 10A to 2A in time 0.1 s, induced emf is 3.28V. What is self-inductance of coil?
A)
4H
done
clear
B)
0.4H
done
clear
C)
0.04H
done
clear
D)
5H
done
clear
View Answer play_arrow
question_answer 38) Resistance of rod is 1\[\Omega \]. It is bent in form of square. What is resistance across adjoint corners?
A)
1\[\Omega \]
done
clear
B)
3\[\Omega \]
done
clear
C)
\[\frac{3}{16}\Omega \]
done
clear
D)
\[\frac{3}{4}\Omega \]
done
clear
View Answer play_arrow
question_answer 39) In a circuit L, C and R are connected in series with an alternating voltage source of frequency \[f\]. The current leads the voltage by \[45{}^\circ \]. The value of C is
A)
\[\frac{1}{2\pi f(2\pi fL+R)}\]
done
clear
B)
\[\frac{1}{\pi f(2\pi fL+R)}\]
done
clear
C)
\[\frac{1}{2\pi f(2\pi fL-R)}\]
done
clear
D)
\[\frac{1}{\pi f(2\pi fL-R)}\]
done
clear
View Answer play_arrow
question_answer 40) What is angle between electric field and equipotential surface?
A)
\[90{}^\circ \text{ }always\]
done
clear
B)
\[0{}^\circ \text{ }always\]
done
clear
C)
\[0{}^\circ \text{ }to\text{ }90{}^\circ \]
done
clear
D)
\[0{}^\circ \text{ }to\text{ }180{}^\circ \]
done
clear
View Answer play_arrow
question_answer 41) A ball falls from 20 m height on floor and rebounds to 5m. Time of contact is 0.02s. Find acceleration during impact.
A)
\[1200\,m/{{s}^{2}}\]
done
clear
B)
\[1000\,m/{{s}^{2}}\]
done
clear
C)
\[2000\,m/{{s}^{2}}\]
done
clear
D)
\[1500\,m/{{s}^{2}}\]
done
clear
View Answer play_arrow
question_answer 42) Two drops of equal radius coalesce to form a bigger drop. What is ratio of surface energy of bigger drop to smaller one?
A)
\[{{2}^{1/2}}:1\]
done
clear
B)
\[1:1\]
done
clear
C)
\[{{2}^{2/3}}:1\]
done
clear
D)
None of these
done
clear
View Answer play_arrow
question_answer 43) In any fission process the ratio \[\frac{mass\,of\,fission\,products}{mass\,of\,parent\,nucleus}is\]
A)
less than 1
done
clear
B)
greater than 1
done
clear
C)
equal to 1
done
clear
D)
depends on the mass of parent nucleus
done
clear
View Answer play_arrow
question_answer 44) In the phenomenon of diffraction of light. when blue light is used in the experiment instead of red light, then
A)
fringes will become narrower
done
clear
B)
fringes will become broader
done
clear
C)
no change in fringe width
done
clear
D)
None of the above
done
clear
View Answer play_arrow
question_answer 45) A glass slab \[(\mu =1.5)\] of thickness 6 cm is placed over a paper. What is the shift in the letters?
A)
4 cm
done
clear
B)
2 cm
done
clear
C)
1 cm
done
clear
D)
None of these
done
clear
View Answer play_arrow
question_answer 46) Two capacitors of capacitance C are connected in series. If one of them is filled with dielectric substance K, what is the effective capacitance?
A)
\[\frac{KC}{(1+K)}\]
done
clear
B)
C (K + 1)
done
clear
C)
\[\frac{2KC}{K+1}\]
done
clear
D)
None of these
done
clear
View Answer play_arrow
question_answer 47) A person is sitting in a lift accelerating upwards. Measured weight of person will be
A)
less than actual weight
done
clear
B)
equal to actual weight
done
clear
C)
more than actual weight
done
clear
D)
None of the above
done
clear
View Answer play_arrow
question_answer 48) By mistake a voltmeter is connected in series and an ammeter is connected in parallel with a resistance in an electrical circuit. What will happen to the instruments?
A)
Voltmeter is damaged
done
clear
B)
Ammeter is damaged
done
clear
C)
Both are damaged
done
clear
D)
None is damaged
done
clear
View Answer play_arrow
question_answer 49) The half-life of \[A{{t}^{215}}\]is 100 \[\mu s\]. If a sample contains 215 mg of \[A{{t}^{215}}\], the activity of the sample initially is
A)
\[{{10}^{2}}Bq\]
done
clear
B)
\[3\times {{10}^{10}}Bq\]
done
clear
C)
\[4.17\times {{10}^{24}}Bq\]
done
clear
D)
\[1.16\times {{10}^{5}}Bq\]
done
clear
View Answer play_arrow
question_answer 50) The ratio of minimum to maximum wavelength in Balmer series is
A)
5 : 9
done
clear
B)
5 : 36
done
clear
C)
1 : 4
done
clear
D)
3 : 4
done
clear
View Answer play_arrow
question_answer 51) A ball is released from the top of a tower. The ratio of work done by force of gravity in first, second and third second of the motion of the ball is
A)
1 : 2 : 3
done
clear
B)
1 : 4 : 9
done
clear
C)
1 : 3 : 5
done
clear
D)
1 : 5 : 3
done
clear
View Answer play_arrow
question_answer 52) A body of mass 2 kg moving with a velocity of 3 m/s collides head on with a body of mass 1 kg moving in opposite direction with a velocity of 4 m/s. After collision two bodies stick together and move with a common velocity which in m/s is equal to
A)
1/4
done
clear
B)
1/3
done
clear
C)
2/3
done
clear
D)
3/4
done
clear
View Answer play_arrow
question_answer 53) Two spheres P and Q, of same colour having radii 8 cm and 2 cm are maintained at temperatures \[127{}^\circ C\] and \[527{}^\circ C\] respectively. The energy radiated by P and Q is
A)
0.054
done
clear
B)
0.0034
done
clear
C)
1
done
clear
D)
2
done
clear
View Answer play_arrow
question_answer 54) A cane is taken out from a refrigerator at \[0{}^\circ C\]. The atmospheric temperature is \[25{}^\circ C\]. If \[{{t}_{1}}\] is the time taken to heat from \[0{}^\circ C\] to \[5{}^\circ C\] and \[{{t}_{2}}\] is the time taken from \[10{}^\circ C\] to \[15{}^\circ C\], then
A)
\[{{t}_{1}}>{{t}_{2}}\]
done
clear
B)
\[{{t}_{1}}<{{t}_{2}}\]
done
clear
C)
\[{{t}_{1}}={{t}_{2}}\]
done
clear
D)
there is no relation
done
clear
View Answer play_arrow
question_answer 55) If an electron and a photon propagate in the form of waves having the same wavelength, it implies that they have the same
A)
energy
done
clear
B)
momentum
done
clear
C)
velocity
done
clear
D)
angular momentum
done
clear
View Answer play_arrow
question_answer 56) The work function of a substance is 4.0 eV. The longest wavelength of light that can cause photoelectron emission from this substance is approximately
A)
540 nm
done
clear
B)
400 nm
done
clear
C)
310nm
done
clear
D)
220 nm
done
clear
View Answer play_arrow
question_answer 57) Work function of a metal is 2.1 eV. Which of the waves of the following wavelengths will be able to emit photoelectrons from its surface?
A)
\[4000\overset{\text{o}}{\mathop{\text{A}}}\,,\,\,7500\overset{\text{o}}{\mathop{\text{A}}}\,\]
done
clear
B)
\[5500\overset{\text{o}}{\mathop{\text{A}}}\,,\,6000\overset{\text{o}}{\mathop{\text{A}}}\,\]
done
clear
C)
\[4000\overset{\text{o}}{\mathop{\text{A}}}\,,\,6000\overset{\text{o}}{\mathop{\text{A}}}\,\]
done
clear
D)
None of the above
done
clear
View Answer play_arrow
question_answer 58) A laser beam of pulse power \[{{10}^{12}}\]W is focused on an object of area\[{{10}^{-4}}c{{m}^{2}}\]. The energy flux in watt/\[c{{m}^{2}}\] at the point of focus is
A)
\[{{10}^{20}}\]
done
clear
B)
\[{{10}^{16}}\]
done
clear
C)
\[{{10}^{8}}\]
done
clear
D)
\[{{10}^{4}}\]
done
clear
View Answer play_arrow
question_answer 59) A laser device produces amplification in the
A)
microwave region
done
clear
B)
ultraviolet or visible region
done
clear
C)
infrared region
done
clear
D)
None of the above
done
clear
View Answer play_arrow
question_answer 60) Which of the following circular rods. (given radius r and length 0 each made of the same material as whose ends are maintained at the same temperature will conduct most heat?
A)
\[r=2{{r}_{0}};l=2{{l}_{0}}\]
done
clear
B)
\[r=2{{r}_{0}};l={{l}_{0}}\]
done
clear
C)
\[r={{r}_{0}};l={{l}_{0}}\]
done
clear
D)
\[r={{r}_{0}};l=2{{l}_{0}}\]
done
clear
View Answer play_arrow
question_answer 61) Which of the following is diamagnetic?
A)
\[H_{2}^{+}\]
done
clear
B)
\[{{O}_{2}}\]
done
clear
C)
\[L{{i}_{2}}\]
done
clear
D)
\[He_{2}^{+}\]
done
clear
View Answer play_arrow
question_answer 62) Which of the following can participate in linkage isomerism?
A)
\[NO_{2}^{-}\]
done
clear
B)
\[{{H}_{2}}\overset{\centerdot \,\,\,\centerdot }{\mathop{N}}\,C{{H}_{2}}C{{H}_{2}}\overset{\centerdot \,\,\,\centerdot }{\mathop{N}}\,{{H}_{2}}\]
done
clear
C)
\[{{H}_{2}}O\]
done
clear
D)
\[:N{{H}_{3}}\]
done
clear
View Answer play_arrow
question_answer 63) By heating phenol with chloroform in alkali, it is converted into
A)
salicylic acid
done
clear
B)
salicylaldehyde
done
clear
C)
anisole
done
clear
D)
phenyl benzoate
done
clear
View Answer play_arrow
question_answer 64) Osmotic pressure observed when benzoic acid is dissolved in benzene is less than that expected from theoretical considerations. This is because
A)
benzoic acid is an organic solute
done
clear
B)
benzoic acid has higher molar mass than benzene
done
clear
C)
benzoic acid gets associated in benzene
done
clear
D)
benzoic acid gets dissociated in benzene
done
clear
View Answer play_arrow
question_answer 65) The formula mass of Moms salt is 392. The iron present in it is oxidized by\[KMn{{O}_{4}}\]in acid medium. The equivalent mass of Mohrs salt is
A)
392
done
clear
B)
31.6
done
clear
C)
278
done
clear
D)
156
done
clear
View Answer play_arrow
question_answer 66) Solubility product of a salt\[AB\]is\[1\times {{10}^{-8}}{{M}^{2}}\]in a solution in which the concentration of\[{{A}^{+}}\]ions is\[{{10}^{-3}}M\]. The salt will precipitate when the concentration of\[{{B}^{-}}\]ions is kept
A)
between\[{{10}^{-8}}M\]to\[{{10}^{-7}}M\]
done
clear
B)
between\[{{10}^{-7}}M\]to\[{{10}^{-8}}M\]
done
clear
C)
\[>{{10}^{-5}}M\]
done
clear
D)
\[<{{10}^{-8}}M\]
done
clear
View Answer play_arrow
question_answer 67) The decomposition of a certain mass of\[CaC{{O}_{3}}\]gave\[11.2\,\,d{{m}^{3}}\]of\[C{{O}_{2}}\]gas at STP. The mass of\[KOH\]required to completely I neutralize the gas is
A)
56 g
done
clear
B)
28 g
done
clear
C)
42 g
done
clear
D)
20 g
done
clear
View Answer play_arrow
question_answer 68) The basicity of aniline is less than that of cyclohexylamine. This is due to
A)
\[+R-\]effect of\[-N{{H}_{2}}\]group
done
clear
B)
\[-I-\]effect of\[-N{{H}_{2}}\]group
done
clear
C)
\[-R-\]effect of\[-N{{H}_{2}}\]group
done
clear
D)
hyperconjugation effect
done
clear
View Answer play_arrow
question_answer 69) A distinctive and characteristic functional group of fats is
A)
a peptide group
done
clear
B)
an ester group
done
clear
C)
an alcoholic group
done
clear
D)
a ketonic group
done
clear
View Answer play_arrow
question_answer 70) Which of the following compound is expected to be optically active?
A)
\[{{(C{{H}_{3}})}_{2}}CHCHO\]
done
clear
B)
\[C{{H}_{3}}C{{H}_{2}}C{{H}_{2}}CHO\]
done
clear
C)
\[C{{H}_{3}}C{{H}_{2}}CHBrCHO\]
done
clear
D)
\[C{{H}_{3}}C{{H}_{2}}CB{{r}_{2}}CHO\]
done
clear
View Answer play_arrow
question_answer 71) Which cycloalkane has the lowest heat of combustion per\[C{{H}_{2}}\]group?
A)
Cyclopropane
done
clear
B)
Cyclobutane
done
clear
C)
Cyclopentane
done
clear
D)
Cyclohexane
done
clear
View Answer play_arrow
question_answer 72) The physical states of dispersing phase and dispersion medium in colloid like pesticide spray respectively, are
A)
gas, liquid
done
clear
B)
solid, gas
done
clear
C)
liquid, solid
done
clear
D)
liquid, gas
done
clear
View Answer play_arrow
question_answer 73) Potassium dichromate is used
A)
in electroplating
done
clear
B)
as a reducing agent
done
clear
C)
it oxidizes ferrous ions into ferric ions in acidic media as an oxidizing agent
done
clear
D)
as an insecticide
done
clear
View Answer play_arrow
question_answer 74) Which one of the following statements is incorrect for the sucrose?
A)
It is obtained from cane sugar
done
clear
B)
It is not reducing sugar
done
clear
C)
On hydrolysis, it gives equal quantities of D-glucose and D-fructose
done
clear
D)
It gives aspartame when it is heated at\[{{210}^{o}}C\]
done
clear
View Answer play_arrow
question_answer 75) Inductive effect involves
A)
displacement of \[\sigma \]-electrons
done
clear
B)
delocalisation of \[\pi \]-electrons
done
clear
C)
delocalisation of \[\sigma \]-electrons
done
clear
D)
displacement of \[\pi \]-electrons
done
clear
View Answer play_arrow
question_answer 76) The atomic number of\[Ni\]and\[Cu\]are 28 and 29 respectively. The electronic configuration \[1{{s}^{2}},\,\,2{{s}^{2}},\,\,2{{p}^{6}},\,\,3{{s}^{2}}\,\,3{{p}^{6}}\,\,3{{d}^{10}}\]represents
A)
\[C{{u}^{+}}\]
done
clear
B)
\[C{{u}^{2+}}\]
done
clear
C)
\[N{{i}^{2+}}\]
done
clear
D)
\[Ni\]
done
clear
View Answer play_arrow
question_answer 77) In which of the following complex ion, the central metal ion is in a state of\[s{{p}^{3}}{{d}^{2}}\]hybridisation?
A)
\[{{[CoF]}^{3-}}\]
done
clear
B)
\[{{[CO{{(N{{H}_{3}})}_{6}}]}^{3+}}\]
done
clear
C)
\[{{[Fe{{(CN)}_{6}}]}^{3-}}\]
done
clear
D)
\[{{[Cr{{(N{{H}_{3}})}_{6}}]}^{3+}}\]
done
clear
View Answer play_arrow
question_answer 78) The formation of\[O_{2}^{+}{{[Pt{{F}_{6}}]}^{-}}\]is the basis for the formation of xenon fluorides. This is because
A)
\[{{O}_{2}}\]and\[Xe\]have comparable sizes
done
clear
B)
Both\[{{O}_{2}}\]and\[Xe\]are gases
done
clear
C)
\[{{O}_{2}}\]and\[Xe\]have comparable ionization energies
done
clear
D)
Both (a) and (c)
done
clear
View Answer play_arrow
question_answer 79) The density of a gas is\[1.964\,\,g\,\,d{{m}^{-3}}\]at\[273\,\,K\]and\[76\,\,cm\,\,Hg\]. The gas is
A)
\[C{{H}_{4}}\]
done
clear
B)
\[{{C}_{2}}{{H}_{6}}\]
done
clear
C)
\[C{{O}_{2}}\]
done
clear
D)
\[Xe\]
done
clear
View Answer play_arrow
question_answer 80) \[\Delta {{G}^{o}}vs\,\,T\]plot in the Ellinghams diagram slopes downwards for the reactions
A)
\[Mg+\frac{1}{2}{{O}_{2}}\xrightarrow{{}}MgO\]
done
clear
B)
\[2Ag+\frac{1}{2}{{O}_{2}}\xrightarrow{{}}A{{g}_{2}}O\]
done
clear
C)
\[CO+\frac{1}{2}{{O}_{2}}\xrightarrow{{}}C{{O}_{2}}\]
done
clear
D)
All of the above
done
clear
View Answer play_arrow
question_answer 81) When a mixture of calcium benzoate and calcium acetate is dry distilled, the resulting compound is
A)
acetophenone
done
clear
B)
benzaldehyde
done
clear
C)
benzophenone
done
clear
D)
acetaldehyde
done
clear
View Answer play_arrow
question_answer 82) In a metallic crystal
A)
the valence electrons constitute a sea of mobile electrons
done
clear
B)
the valence electrons are localized in between the kernels
done
clear
C)
the valence electrons remain within the field of influence of their own kernels
done
clear
D)
None of the above
done
clear
View Answer play_arrow
question_answer 83) Which of the following is correct, based on molecular orbital theory for peroxide ion?
A)
Its bond order is one and it is paramagnetic
done
clear
B)
Its bond order is two and it is diamagnetic
done
clear
C)
Its bond order is one and it is diamagnetic
done
clear
D)
Its bond order is two and it is paramagnetic
done
clear
View Answer play_arrow
question_answer 84) Insulin regulates the metabolism of
A)
minerals
done
clear
B)
ammo acids
done
clear
C)
glucose
done
clear
D)
vitamins
done
clear
View Answer play_arrow
question_answer 85) Which of the following electrolyte will have maximum flocculation value for\[Fe{{(OH)}_{3}}\]sol?
A)
\[NaCl\]
done
clear
B)
\[N{{a}_{2}}S\]
done
clear
C)
\[{{(N{{H}_{4}})}_{3}}P{{O}_{4}}\]
done
clear
D)
\[{{K}_{2}}S{{O}_{4}}\]
done
clear
View Answer play_arrow
question_answer 86) The concentration of a reactant X decreases from\[0.1M\]to\[0.005M\]in 40 min. If the reaction follows first order kinetics, the rate of the reaction when the concentration of\[X\]is \[0.01\,\,M\]will be
A)
\[1.73\times {{10}^{-4}}M\,\,{{\min }^{-1}}\]
done
clear
B)
\[3.47\times {{10}^{-4}}M\,\,{{\min }^{-1}}\]
done
clear
C)
\[3.47\times {{10}^{-5}}M\,\,{{\min }^{-1}}\]
done
clear
D)
\[7.5\times {{10}^{-4}}M\,\,{{\min }^{-1}}\]
done
clear
View Answer play_arrow
question_answer 87) At\[pH=4\], glycine exists as
A)
\[{{H}_{3}}N-C{{H}_{2}}-CO{{O}^{-}}\]
done
clear
B)
\[{{H}_{3}}N-C{{H}_{2}}-COOH\]
done
clear
C)
\[{{H}_{2}}N-C{{H}_{2}}-COOH\]
done
clear
D)
\[{{H}_{2}}N-C{{H}_{2}}-CO{{O}^{-}}\]
done
clear
View Answer play_arrow
question_answer 88) Which of the following taking place in the blast furnace is endothermic?
A)
\[CaC{{O}_{3}}\xrightarrow{{}}CaO+C{{O}_{2}}\]
done
clear
B)
\[2C+{{O}_{2}}\xrightarrow{{}}2CO\]
done
clear
C)
\[C+{{O}_{2}}\xrightarrow{{}}C{{O}_{2}}\]
done
clear
D)
\[F{{e}_{2}}{{O}_{3}}+3CO\xrightarrow{{}}2Fe+3C{{O}_{2}}\]
done
clear
View Answer play_arrow
question_answer 89) The\[emf\,\,{{E}^{o}}\]of the following cells are: \[AG|A{{g}^{+}}(1M)||C{{u}^{2+}}(1M)|Cu;\,\,{{E}^{o}}=-0.46\,\,V\] \[Zn|Z{{n}^{2+}}(1M)||C{{u}^{2+}}(1M)|Cu;\,\,{{E}^{o}}=1.10\,\,V\] emf of the following cell is \[Zn|Z{{n}^{2+}}(1M)||A{{g}^{+}}(1M)|Ag\]
A)
\[0.64\,\,V\]
done
clear
B)
\[1.10\,\,V\]
done
clear
C)
\[1.56\,\,V\]
done
clear
D)
\[-0.64\,\,V\]
done
clear
View Answer play_arrow
question_answer 90) The formation of cyanohydrin from acetone is which type of reaction?
A)
Electrophilic substitution reaction
done
clear
B)
Electrophilic addition reaction
done
clear
C)
Nucleophilic addition reaction
done
clear
D)
Nucleophilic substitution reaction
done
clear
View Answer play_arrow
question_answer 91) Name the end product in the following series of reactions \[C{{H}_{3}}COOH\xrightarrow{N{{H}_{3}}}A\xrightarrow{Heat}B\xrightarrow[\Delta ]{{{P}_{4}}{{O}_{14}}}C\]
A)
\[C{{H}_{3}}OH\]
done
clear
B)
\[C{{H}_{4}}\]
done
clear
C)
\[C{{H}_{3}}COON{{H}_{4}}\]
done
clear
D)
\[C{{H}_{3}}CN\]
done
clear
View Answer play_arrow
question_answer 92) The presence of unpaired electron in phosphorous atom is explained by which principle?
A)
Aufbau principle
done
clear
B)
Faults exclusion principle
done
clear
C)
Hunds rule
done
clear
D)
Heisenbergs principle
done
clear
View Answer play_arrow
question_answer 93) If a cricket ball having mass of\[200\,\,g\]is thrown with a speed of\[3\times {{10}^{3}}\,\,cm/s\], then calculate the wavelength related to it.
A)
\[2.2\times {{10}^{-27}}cm\]
done
clear
B)
\[1.104\times {{10}^{-32}}cm\]
done
clear
C)
\[1.104\times {{10}^{-32}}cm\]
done
clear
D)
\[1.104\times {{10}^{-33}}cm\]
done
clear
View Answer play_arrow
question_answer 94) Which type of stacking pattern is found in sodium chloride crystal lattice?
A)
\[a-b-a-b\]
done
clear
B)
\[a-a-a\]
done
clear
C)
\[a-b-c-a-b-c\]
done
clear
D)
None of these
done
clear
View Answer play_arrow
question_answer 95) Equivalent weight of a bivalent metal is 37.2. The molecular weight of its chloride is
A)
412.2
done
clear
B)
216
done
clear
C)
145.4
done
clear
D)
108.2
done
clear
View Answer play_arrow
question_answer 96) Phenolphthalein is obtained by heating phthalic anhydride with \[conc.{{H}_{2}}S{{O}_{4}}\]and
A)
benzyl alcohol
done
clear
B)
benzene
done
clear
C)
phenol
done
clear
D)
benzoic acid
done
clear
View Answer play_arrow
question_answer 97) Freezing point of urea solution is\[-{{0.6}^{o}}C\]. How much urea\[(m.wt.=60g/mol)\]will be required to dissolve in 3 kg water? \[({{k}_{f}}={{1.5}^{o}}C\,\,kg\,\,mo{{l}^{-1}})\]
A)
24 g
done
clear
B)
36 g
done
clear
C)
60 g
done
clear
D)
72 g
done
clear
View Answer play_arrow
question_answer 98) If\[K<1.0\], what will be the value of\[\Delta {{G}^{o}}\]of the following?
A)
Zero
done
clear
B)
1.0
done
clear
C)
Positive
done
clear
D)
Negative
done
clear
View Answer play_arrow
question_answer 99) The normality of a solution containing 32.5 g of\[{{(COOH)}_{2}}\cdot 2{{H}_{2}}O\]per\[0.5\,\,L\]is
A)
\[10\,\,N\]
done
clear
B)
\[1\,\,N\]
done
clear
C)
\[2\,\,N\]
done
clear
D)
\[0.1\,\,N\]
done
clear
View Answer play_arrow
question_answer 100) For the titration of\[KOH\]vs\[{{(COOH)}_{2}}\cdot 2{{H}_{2}}O\], the suitable indicator is
A)
methyl orange
done
clear
B)
phenolphthalein
done
clear
C)
methyl red
done
clear
D)
All can be used
done
clear
View Answer play_arrow
question_answer 101) The radius of\[N{{a}^{+}}\]is\[95\,\,\text{pm}\]and that of\[C{{l}^{-}}\]ion is\[181\,\,\text{pm}\]. The coordination number of\[N{{a}^{+}}\]is
A)
8
done
clear
B)
6
done
clear
C)
4
done
clear
D)
unpredictable
done
clear
View Answer play_arrow
question_answer 102) In van der Waals equation of state of the gas law, the constant V is a measure of
A)
intermolecular repulsion
done
clear
B)
intermolecular attraction
done
clear
C)
volume occupied by the molecules
done
clear
D)
intermolecular collisions per unit volume
done
clear
View Answer play_arrow
question_answer 103) Which reaction intermediate is formed during the condensation reaction between acetaldehyde and formaldehyde?
A)
\[:C{{H}_{2}}CHO\]
done
clear
B)
\[\overset{+}{\mathop{C}}\,{{H}_{2}}CHO\]
done
clear
C)
\[\overset{+}{\mathop{C}}\,{{H}_{2}}OH\]
done
clear
D)
\[:\bar{C}HCHO\]
done
clear
View Answer play_arrow
question_answer 104) \[2,\,\,2\mathbf{-}\]dichloro propane on hydrolysis yields
A)
acetone
done
clear
B)
\[2,\,\,2\mathbf{-}\]propane diol
done
clear
C)
iso-propyl alcohol
done
clear
D)
acetaldehyde
done
clear
View Answer play_arrow
question_answer 105) Phenols are more acidic than alcohols because
A)
phenoxide ion is stabilized by resonance
done
clear
B)
phenols are more soluble in polar solvents
done
clear
C)
phenoxide ions do not exhibit resonance
done
clear
D)
alcohols do not lose H atoms at all
done
clear
View Answer play_arrow
question_answer 106) Lemon gives sour taste because of
A)
citric acid
done
clear
B)
tartaric acid
done
clear
C)
oxalic acid
done
clear
D)
acetic acid
done
clear
View Answer play_arrow
question_answer 107) When ammonium chloride is added to ammonia solution, the pH of the resulting solution will be
A)
increased
done
clear
B)
seven
done
clear
C)
decreased
done
clear
D)
unchanged
done
clear
View Answer play_arrow
question_answer 108) Which of the following has highest second ionization energy?
A)
Calcium
done
clear
B)
Chromium
done
clear
C)
Iron
done
clear
D)
Cobalt
done
clear
View Answer play_arrow
question_answer 109) The standard reduction potentials at\[298K\]for the following half-cell reactions are given below \[Z{{n}^{2+}}(aq)+2{{e}^{-}}Zn(s)-0.762\] \[C{{r}^{3+}}(aq)+3{{e}^{-}}Cr(s)-0.74\] \[2{{H}^{+}}(aq)+2{{e}^{-}}{{H}_{2}}(g)-0.00\] \[F{{e}^{3+}}(aq)+{{e}^{-}}F{{e}^{2+}}(aq)-0.77\] Which one of the following is the strongest reducing agent?
A)
\[Zn(s)\]
done
clear
B)
\[Cr(s)\]
done
clear
C)
\[{{H}_{2}}(g)\]
done
clear
D)
\[F{{e}^{2+}}(aq)\]
done
clear
View Answer play_arrow
question_answer 110) Following reaction, \[{{(C{{H}_{3}})}_{3}}CBr+{{H}_{2}}O\xrightarrow{{}}{{(C{{H}_{3}})}_{3}}COH+HBr\]is an example of
A)
elimination reaction
done
clear
B)
free radical substitution
done
clear
C)
nucleophilic substitution
done
clear
D)
electrophilic substitution
done
clear
View Answer play_arrow
question_answer 111) The unit of rate for a first order reaction is
A)
\[L\,\,{{s}^{-1}}\]
done
clear
B)
\[mo{{l}^{-1}}\,\,L\,\,{{s}^{-1}}\]
done
clear
C)
\[mol\,\,{{L}^{-1}}\,\,{{s}^{-1}}\]
done
clear
D)
\[mol\,\,{{s}^{-1}}\]
done
clear
View Answer play_arrow
question_answer 112) \[Iso-\]propyl amine with excess of acetyl chloride will give
A)
\[{{(C{{H}_{3}}CO)}_{2}}N-C-{{(C{{H}_{3}})}_{3}}\]
done
clear
B)
\[{{(C{{H}_{3}})}_{2}}CH-\underset{\begin{smallmatrix} | \\ H \end{smallmatrix}}{\mathop{N}}\,-COC{{H}_{3}}\]
done
clear
C)
\[{{(C{{H}_{3}})}_{2}}CHN{{(CO{{H}_{3}})}_{2}}\]
done
clear
D)
\[C{{H}_{3}}C{{H}_{2}}C{{H}_{2}}-\underset{\begin{smallmatrix} | \\ H \end{smallmatrix}}{\mathop{N}}\,-COC{{H}_{3}}\]
done
clear
View Answer play_arrow
question_answer 113) \[{{C}_{2}}{{H}_{5}}CHO\]and\[{{(C{{H}_{3}})}_{2}}CO\]can be distinguished by testing with
A)
phenyl hydrazine
done
clear
B)
hydroxyl amine
done
clear
C)
Fehling solution
done
clear
D)
sodium bisulphite
done
clear
View Answer play_arrow
question_answer 114) Glucose molecule reacts with\[X\]number of molecules of phenylhydrazine to yield osazone. The value of T is
A)
four
done
clear
B)
one
done
clear
C)
two
done
clear
D)
three
done
clear
View Answer play_arrow
question_answer 115) The oxidation number of chromium in\[Cr{{O}_{5}}\]is
A)
+3
done
clear
B)
+ 5
done
clear
C)
+ 10
done
clear
D)
+ 6
done
clear
View Answer play_arrow
question_answer 116) Liquor ammonia bottles are opened only after cooling. This is because
A)
it is a mild explosive
done
clear
B)
it generates high vapour pressure
done
clear
C)
Both (a) and (b)
done
clear
D)
it is lachrymatory
done
clear
View Answer play_arrow
question_answer 117) What will be the proportion of moles of metal \[(Cu:Ni:Ag)\]at cathode according to the second law of Faraday?
A)
\[1:2:1\]
done
clear
B)
\[2:2:1\]
done
clear
C)
\[1:2:2\]
done
clear
D)
\[1:1:2\]
done
clear
View Answer play_arrow
question_answer 118) Which equation is true to calculate the energy of activation, if the rate of reaction is doubled by increasing temperature from\[{{T}_{1}}K\]to\[{{T}_{2}}K\]?
A)
\[{{\log }_{10}}\frac{{{k}_{1}}}{{{k}_{2}}}=\frac{{{E}_{a}}}{2.303R}\left[ \frac{1}{{{T}_{1}}}-\frac{1}{{{T}_{2}}} \right]\]
done
clear
B)
\[{{\log }_{10}}\frac{{{k}_{2}}}{{{k}_{1}}}=\frac{{{E}_{a}}}{2.303R}\left[ \frac{1}{{{T}_{2}}}-\frac{1}{{{T}_{1}}} \right]\]
done
clear
C)
\[{{\log }_{10}}\frac{1}{2}=\frac{{{E}_{a}}}{2.303}\left[ \frac{1}{{{T}_{2}}}-\frac{1}{{{T}_{1}}} \right]\]
done
clear
D)
\[{{\log }_{10}}2=\frac{{{E}_{a}}}{2.303R}\left[ \frac{1}{{{T}_{1}}}-\frac{1}{{{T}_{2}}} \right]\]
done
clear
View Answer play_arrow
question_answer 119) For a reversible reaction : \[X(g)+3Y(g)2Z(g);\,\,\Delta H=-40kJ\] the standard entropies of\[X,\,\,Y\]and\[Z\]are 60, 40 and 50 \[J{{K}^{-1}}mo{{l}^{-1}}\]respectively. The temperature at which the above reaction attains equilibrium is about
A)
\[400\,\,K\]
done
clear
B)
\[500\,\,K\]
done
clear
C)
\[273\,\,K\]
done
clear
D)
\[373\,\,K\]
done
clear
View Answer play_arrow
question_answer 120) Which of the following gives aldol condensation reaction?
A)
\[{{C}_{6}}{{H}_{5}}OH\]
done
clear
B)
\[{{C}_{6}}{{H}_{5}}-\overset{\begin{smallmatrix} O \\ || \end{smallmatrix}}{\mathop{C}}\,-{{C}_{6}}{{H}_{5}}\]
done
clear
C)
\[C{{H}_{3}}C{{H}_{2}}-\overset{\begin{smallmatrix} O \\ || \end{smallmatrix}}{\mathop{C}}\,-C{{H}_{3}}\]
done
clear
D)
\[{{(C{{H}_{3}})}_{3}}C-\overset{\begin{smallmatrix} O \\ || \end{smallmatrix}}{\mathop{C}}\,-{{C}_{6}}{{H}_{5}}\]
done
clear
View Answer play_arrow
question_answer 121) The range of the function\[f\left( x \right)={{x}^{2}}+\frac{1}{{{x}^{2}}+1}\]is
A)
\[[1,\,\,\infty )\]
done
clear
B)
\[[2,\,\,\infty )\]
done
clear
C)
\[\left[ \frac{3}{2},\,\,\infty \right)\]
done
clear
D)
None of these
done
clear
View Answer play_arrow
question_answer 122) If\[f\left( x \right)=\left\{ \begin{matrix} a{{x}^{2}}+b, & b\ne 0,\,\,x\le 1 \\ b{{x}^{2}}+ax+c, & x>1 \\ \end{matrix} \right.\],then \[f\left( x \right)\]is continuous and differentiable at\[x=1\], if
A)
\[c=0,\,\,a=2b\]
done
clear
B)
\[a=b,\,\,c\in R\]
done
clear
C)
\[a=b,\,\,c=0\]
done
clear
D)
\[a=b,\,\,c\ne 0\]
done
clear
View Answer play_arrow
question_answer 123) If a circle passes through the point\[(1,\,\,2)\]and cuts the circle\[{{x}^{2}}+{{y}^{2}}=4\]orthogonally, then the equation of the locus of its centre is
A)
\[{{x}^{2}}+{{y}^{2}}-3x-8y+1=0\]
done
clear
B)
\[{{x}^{2}}+{{y}^{2}}-2x-6y-7=0\]
done
clear
C)
\[2x+4y-9=0\]
done
clear
D)
\[2x+4y-1=0\]
done
clear
View Answer play_arrow
question_answer 124) If\[\int{f\left( x \right)}\sin x\cos x\,\,dx\] \[=\frac{1}{2({{b}^{2}}-{{a}^{2}})}\log [f(x)]+c,\] then\[f\left( x \right)\]is equal to
A)
\[\frac{1}{{{a}^{2}}{{\sin }^{2}}x+{{b}^{2}}{{\cos }^{2}}x}\]
done
clear
B)
\[\frac{1}{{{a}^{2}}{{\sin }^{2}}x-{{b}^{2}}{{\cos }^{2}}x}\]
done
clear
C)
\[\frac{1}{{{a}^{2}}{{\cos }^{2}}x-{{b}^{2}}{{\sin }^{2}}x}\]
done
clear
D)
\[\frac{1}{{{a}^{2}}{{\cos }^{2}}x+{{b}^{2}}{{\sin }^{2}}x}\]
done
clear
View Answer play_arrow
question_answer 125) The points representing complex number 2 for which\[\left| z-3 \right|=\left| z-5 \right|\]lie on the locus given by
A)
an ellipse
done
clear
B)
a circle
done
clear
C)
a straight line
done
clear
D)
None of the above
done
clear
View Answer play_arrow
question_answer 126) The value of\[\alpha \], for which the equation\[{{x}^{2}}-(\sin \alpha -2)x-(1+\sin \alpha )=0\]has roots whose sum of square is least, is
A)
\[\frac{\pi }{3}\]
done
clear
B)
\[\frac{\pi }{4}\]
done
clear
C)
\[\frac{\pi }{2}\]
done
clear
D)
\[\frac{\pi }{6}\]
done
clear
View Answer play_arrow
question_answer 127) For\[n\in N,\,\,{{10}^{n-2}}\ge 81n\], is
A)
\[n>5\]
done
clear
B)
\[n\ge 5\]
done
clear
C)
\[n<5\]
done
clear
D)
\[n>8\]
done
clear
View Answer play_arrow
question_answer 128) The two consecutive terms in the expansion of\[{{(3+2x)}^{74}}\]whose coefficients are equal are
A)
11, 12
done
clear
B)
7, 8
done
clear
C)
30, 31
done
clear
D)
None of these
done
clear
View Answer play_arrow
question_answer 129) The value of\[2.\overline{357}\]is
A)
\[\frac{2355}{999}\]
done
clear
B)
\[\frac{2355}{1000}\]
done
clear
C)
\[\frac{2355}{1111}\]
done
clear
D)
None of these
done
clear
View Answer play_arrow
question_answer 130) Let\[{{S}_{n}}=\frac{1}{{{1}^{3}}}+\frac{1}{{{1}^{3}}}+\frac{2}{{{2}^{3}}}+...+\frac{1+2+...+n}{{{1}^{3}}+{{2}^{3}}+...+n}\] \[n=1,2,3,...\]. Then,\[{{S}_{n}}\]is not greater than
A)
\[\frac{1}{2}\]
done
clear
B)
1
done
clear
C)
2
done
clear
D)
4
done
clear
View Answer play_arrow
question_answer 131) If\[E(\theta )=\left[ \begin{matrix} {{\cos }^{2}}\theta & \cos \theta \sin \theta \\ \cos \theta \sin \theta & {{\sin }^{2}}\theta \\ \end{matrix} \right]\]and\[\theta \]and\[\phi \] differ by an odd multiple of\[\frac{\pi }{2}\], then\[E(\theta )E(\phi )\]is a
A)
unit matrix
done
clear
B)
null matrix
done
clear
C)
diagonal matrix
done
clear
D)
None of the above
done
clear
View Answer play_arrow
question_answer 132) A parabola is drawn with its focus at\[(3,\,\,4)\]and vertex at the focus of the parabola\[{{y}^{2}}-12x-4y+4=0\]. The equation of the parabola is
A)
\[{{y}^{2}}-8x-6y+25=0\]
done
clear
B)
\[{{y}^{2}}-6x+8y-25=0\]
done
clear
C)
\[{{x}^{2}}-6x-8y+25=0\]
done
clear
D)
\[{{x}^{2}}+6x-8y-25=0\]
done
clear
View Answer play_arrow
question_answer 133) If\[p,\,\,p\]denote the lengths of the perpendiculars from the focus and the centre of an ellipse with semi major axis of length a respectively on a tangent to the ellipse and\[r\]denotes the focal distance of the point, then
A)
\[ap=rp+1\]
done
clear
B)
\[rp=ap\]
done
clear
C)
\[ap=rp+1\]
done
clear
D)
\[ap=rp\]
done
clear
View Answer play_arrow
question_answer 134) The equation of perpendicular bisectors of sides\[AB\]and\[AC\]of a\[\Delta ABC\]are\[x-y+5=0\] and\[x+2y=0\]respectively. If the coordinates of vertex\[A\]are\[(1,\,\,-2)\], the equation of\[BC\]is
A)
\[14x+23y-40=0\]
done
clear
B)
\[14x-23y+40=0\]
done
clear
C)
\[23x+14y-40=0\]
done
clear
D)
\[23x-14y+40=0\]
done
clear
View Answer play_arrow
question_answer 135) If\[\cos \theta =-\frac{\sqrt{3}}{2}\]and\[\sin \alpha =-\frac{3}{5}\], where\[\theta \]does not lie in the third quadrant, then \[\frac{2\tan \alpha +\sqrt{3}\tan \theta }{{{\cot }^{2}}\theta +\cos \alpha }\]is equal to
A)
\[\frac{7}{22}\]
done
clear
B)
\[\frac{5}{22}\]
done
clear
C)
\[\frac{9}{22}\]
done
clear
D)
\[\frac{22}{5}\]
done
clear
View Answer play_arrow
question_answer 136) A parallelogram is constructed on the vectors \[\overset{\to }{\mathop{\mathbf{a}}}\,=3\overset{\to }{\mathop{\alpha }}\,-\overset{\to }{\mathop{\beta }}\,,\,\,\overset{\to }{\mathop{\mathbf{b}}}\,=\overset{\to }{\mathop{\alpha }}\,+3\overset{\to }{\mathop{\beta }}\,\], if\[\left| \overset{\to }{\mathop{\alpha }}\, \right|=\left| \overset{\to }{\mathop{\beta }}\, \right|=2\]and angle between\[\overset{\to }{\mathop{\alpha }}\,\]and\[\overset{\to }{\mathop{\beta }}\,\]is\[\frac{\pi }{3}\], then length of a diagonal of the parallelogram is
A)
\[4\sqrt{5}\]
done
clear
B)
\[4\sqrt{3}\]
done
clear
C)
\[4\sqrt{17}\]
done
clear
D)
None of the above
done
clear
View Answer play_arrow
question_answer 137) The value of\[c\], so that for all real\[x\], the vectors\[cx\widehat{\mathbf{i}}-6\widehat{\mathbf{j}}+3\widehat{\mathbf{k}}\],\[x\widehat{\mathbf{i}}+2\widehat{\mathbf{j}}+2cx\widehat{\mathbf{k}}\]make an obtuse angle, are
A)
\[c<0\]
done
clear
B)
\[0<c<\frac{4}{3}\]
done
clear
C)
\[-\frac{4}{3}<c<0\]
done
clear
D)
\[c>0\]
done
clear
View Answer play_arrow
question_answer 138) The solution of the equation \[y-x\frac{dy}{dx}=a\left( {{y}^{2}}+\frac{dy}{dx} \right)\]
A)
\[y=c(x+a)(1-ay)\]
done
clear
B)
\[y=c(x+a)(1+ay)\]
done
clear
C)
\[y=c(x-a)(1+ay)\]
done
clear
D)
None of the above
done
clear
View Answer play_arrow
question_answer 139) The order of the differential equation whose general solution is given by\[y=({{c}_{1}}+{{c}_{2}})\cos (x+{{c}_{3}})-{{c}_{4}}{{e}^{x\_{{c}_{5}}}}\], where\[{{c}_{1}},\,\,{{c}_{2}},\,\,{{c}_{3}},\,\,{{c}_{4}},\,\,{{c}_{5}}\]are arbitrary constants, is
A)
4
done
clear
B)
3
done
clear
C)
2
done
clear
D)
5
done
clear
View Answer play_arrow
question_answer 140) If\[f(x)={{x}^{3}}+b{{x}^{2}}+cx+d\]and\[0<{{b}^{2}}<c\], then in\[(-\infty ,\,\,\infty )\]
A)
\[f(x)\]is strictly increasing function
done
clear
B)
\[f(x)\]has a local maxima
done
clear
C)
\[f(x)\]strictly decreasing function
done
clear
D)
\[f(x)\]is bounded
done
clear
View Answer play_arrow
question_answer 141) \[\frac{d}{dx}{{\sin }^{-1}}(x\sqrt{1-x}+\sqrt{x}\sqrt{1-{{x}^{2}}})\]
A)
\[-\frac{1}{2x\sqrt{1-x}}-\frac{1}{\sqrt{1-{{x}^{2}}}}\]
done
clear
B)
\[\frac{1}{2\sqrt{x}\sqrt{1-x}}-\frac{1}{\sqrt{1-{{x}^{2}}}}\]
done
clear
C)
\[\frac{1}{2\sqrt{x}\sqrt{1-x}}+\frac{1}{\sqrt{1-{{x}^{2}}}}\]
done
clear
D)
\[-\frac{1}{2\sqrt{x}\sqrt{1-x}}+\frac{1}{\sqrt{1-{{x}^{2}}}}\]
done
clear
View Answer play_arrow
question_answer 142) \[\int{\frac{x{{\tan }^{-1}}x}{{{(1+{{x}^{2}})}^{3}}}}dx\]is equal to
A)
\[\frac{x-{{\tan }^{-1}}x}{1-{{x}^{2}}}+c\]
done
clear
B)
\[\frac{x+{{\tan }^{-1}}x}{\sqrt{1-{{x}^{2}}}}+c\]
done
clear
C)
\[\frac{x-{{\tan }^{-1}}x}{\sqrt{1+{{x}^{2}}}}+c\]
done
clear
D)
\[\frac{x+\sqrt{1-{{x}^{2}}}}{\sqrt{1+{{x}^{2}}}}+c\]
done
clear
View Answer play_arrow
question_answer 143) Let\[A=\left[ \begin{matrix} 1 & \sin \theta & 1 \\ -\sin \theta & 1 & \sin \theta \\ -1 & -\sin \theta & 1 \\ \end{matrix} \right]\], where\[0\le \theta \le 2\pi \]. Then, the range of\[\left| A \right|\]is
A)
0
done
clear
B)
{2, 4}
done
clear
C)
[2, 4]
done
clear
D)
None of the above
done
clear
View Answer play_arrow
question_answer 144) If\[y=\left| \cos x \right|+\left| \sin x \right|\], then\[\frac{dy}{dx}\]at\[x=\frac{2\pi }{3}\]is
A)
0
done
clear
B)
1
done
clear
C)
\[\frac{1-\sqrt{3}}{2}\]
done
clear
D)
\[\frac{\sqrt{3}-1}{2}\]
done
clear
View Answer play_arrow
question_answer 145) \[\underset{n\to \infty }{\mathop{\lim }}\,\left( \frac{1}{1-{{n}^{2}}}+\frac{2}{1-{{n}^{2}}}+...+\frac{n}{1-{{n}^{2}}} \right)\]is equal to
A)
0
done
clear
B)
\[-\frac{1}{2}\]
done
clear
C)
\[\frac{1}{2}\]
done
clear
D)
None of these
done
clear
View Answer play_arrow
question_answer 146) Let\[f(x)=\left\{ \begin{matrix} \sin x, & x\ne n\pi \\ 2 & x=n\pi \\ \end{matrix} \right.\], where\[n\in I\]and\[g(x)=\left\{ \begin{matrix} {{x}^{2}}+1, & x\ne 2 \\ 3, & x=2 \\ \end{matrix} \right.\], then\[\underset{x\to 0}{\mathop{\lim }}\,g[f(x)]\]is
A)
1
done
clear
B)
0
done
clear
C)
3
done
clear
D)
does not exist
done
clear
View Answer play_arrow
question_answer 147) The intercept made by the tangent to the curve\[y=\int_{0}^{x}{|t|}\,\,dt\],which is parallel to the line \[y=2x\], on x-axis is equal to
A)
1
done
clear
B)
-2
done
clear
C)
2
done
clear
D)
None of these
done
clear
View Answer play_arrow
question_answer 148) If\[P={{x}^{3}}-\frac{1}{{{x}^{3}}}\]and\[Q=x-\frac{1}{x},\,\,x\in (0,\,\,x)\], then minimum value of\[\frac{P}{{{Q}^{2}}}\]is
A)
\[2\sqrt{3}\]
done
clear
B)
\[-2\sqrt{3}\]
done
clear
C)
does not exist
done
clear
D)
None of these
done
clear
View Answer play_arrow
question_answer 149) Locus of the point which divides double ordinate of the ellipse\[\frac{{{x}^{2}}}{{{a}^{2}}}+\frac{{{y}^{2}}}{{{b}^{2}}}=1\]in the ratio 1:2 internally, is
A)
\[\frac{{{x}^{2}}}{{{a}^{2}}}-\frac{9{{y}^{2}}}{{{b}^{2}}}=\frac{1}{9}\]
done
clear
B)
\[\frac{{{x}^{2}}}{{{a}^{2}}}+\frac{9{{y}^{2}}}{{{b}^{2}}}=1\]
done
clear
C)
\[\frac{9{{y}^{2}}}{{{a}^{2}}}+\frac{9{{y}^{2}}}{{{b}^{2}}}=1\]
done
clear
D)
None of these
done
clear
View Answer play_arrow
question_answer 150) From any point on the hyperbola\[\frac{{{x}^{2}}}{{{a}^{2}}}-\frac{{{y}^{2}}}{{{b}^{2}}}=1\]tangents are drawn to the hyperbola\[\frac{{{x}^{2}}}{{{a}^{2}}}-\frac{{{y}^{2}}}{{{b}^{2}}}=2\]. The area cut-off by the chord of contact on the asymptotes is equal to
A)
\[\frac{ab}{2}\]
done
clear
B)
\[ab\]
done
clear
C)
\[2ab\]
done
clear
D)
\[4ab\]
done
clear
View Answer play_arrow
question_answer 151) The value of the sum of the series\[3{{\cdot }^{n}}{{C}_{0}}-8{{\cdot }^{n}}{{C}_{1}}+{{13}^{n}}{{C}_{2}}-18{{\cdot }^{n}}{{C}_{3}}+...\]upto\[(n+1)\]terms is
A)
0
done
clear
B)
\[{{3}^{n}}\]
done
clear
C)
\[{{5}^{n}}\]
done
clear
D)
None of these
done
clear
View Answer play_arrow
question_answer 152) If\[A\]is a skew-symmetric matrix, then trace of\[A\]is
A)
1
done
clear
B)
-1
done
clear
C)
0
done
clear
D)
None of these
done
clear
View Answer play_arrow
question_answer 153) The arbitrary constant on which the value of the determinant \[\left| \begin{matrix} 1 & \alpha & {{\alpha }^{2}} \\ \cos (p-d)a & \cos pa & \cos (p-d)a \\ \sin (p-d)a & \sin pa & \sin (p-d)a \\ \end{matrix} \right|\]does not depend, is
A)
\[\alpha \]
done
clear
B)
p
done
clear
C)
d
done
clear
D)
a
done
clear
View Answer play_arrow
question_answer 154) The sum of the first n terms of the series\[\frac{1}{2}+\frac{3}{4}+\frac{7}{8}+\frac{15}{16}+...\]is equal to
A)
\[{{2}^{n}}-n+1\]
done
clear
B)
\[1-{{2}^{n}}\]
done
clear
C)
\[n+{{2}^{-n}}-1\]
done
clear
D)
\[{{2}^{n}}-1\]
done
clear
View Answer play_arrow
question_answer 155) The base of a cliff is circular. From the extremities of a diameter of the base angles of elevation of the top of the cliff are \[{{30}^{o}}\]and\[{{60}^{o}}\]. If the height of the cliff be 500 m, then the diameter of the base of the cliff is
A)
\[\frac{2000}{\sqrt{3}}m\]
done
clear
B)
\[\frac{1000}{\sqrt{3}}m\]
done
clear
C)
\[\frac{2000}{\sqrt{3}}m\]
done
clear
D)
\[1000\sqrt{3}\,m\]
done
clear
View Answer play_arrow
question_answer 156) The most general solutions of the equation\[\sec x-1=(\sqrt{2}-1)\tan x\]are given by
A)
\[n\pi +\frac{\pi }{8}\]
done
clear
B)
\[2n\pi ,\,\,2n\pi +\frac{\pi }{4}\]
done
clear
C)
\[2n\pi \]
done
clear
D)
None of these
done
clear
View Answer play_arrow
question_answer 157) The maximum value of\[\sin \left( x+\frac{\pi }{6} \right)+\cos \left( x+\frac{\pi }{6} \right)\]in the interval \[\left( 0,\,\frac{\pi }{2} \right)\] is attained at
A)
\[x=\frac{\pi }{12}\]
done
clear
B)
\[x=\frac{\pi }{6}\]
done
clear
C)
\[x=\frac{\pi }{3}\]
done
clear
D)
\[x=\frac{\pi }{2}\]
done
clear
View Answer play_arrow
question_answer 158) If\[{{z}_{r}}=\cos \frac{r\alpha }{{{n}^{2}}}+i\sin \frac{r\alpha }{2}\], where\[r=1,\,\,2,\,\,3,....,\,\,n,\]then\[\underset{n\to \infty }{\mathop{\lim }}\,\,\,{{z}_{1}},\,\,{{z}_{2}}...{{z}_{n}}\]is equal to
A)
\[\cos \alpha +i\sin \alpha \]
done
clear
B)
\[\cos \left( \frac{\alpha }{2} \right)-i\sin \left( \frac{\alpha }{2} \right)\]
done
clear
C)
\[{{e}^{i\alpha /2}}\]
done
clear
D)
\[\sqrt[3]{{{e}^{i\alpha }}}\]
done
clear
View Answer play_arrow
question_answer 159) Negation of Paris is in France and London is in England is
A)
Paris is in England and London is in France
done
clear
B)
Paris is not in France or London is not in England
done
clear
C)
Paris is in England or London is in France
done
clear
D)
None of the above
done
clear
View Answer play_arrow
question_answer 160) The area enclosed between the curves\[y={{x}^{3}}\]and\[y=\sqrt{x}\]is
A)
\[\frac{5}{3}sq\,\,unit\]
done
clear
B)
\[\frac{5}{4}sq\,\,unit\]
done
clear
C)
\[\frac{5}{12}sq\,\,unit\]
done
clear
D)
\[\frac{12}{5}sq\,\,unit\]
done
clear
View Answer play_arrow
question_answer 161) Find the equation of the bisector of the obtuse angle between the lines\[3x-4y+7=0\]and\[-12x-5y+2=0\],
A)
\[21x+77y-101=0\]
done
clear
B)
\[99x-27y+81=0\]
done
clear
C)
\[21x-77y+101=0\]
done
clear
D)
None of the above
done
clear
View Answer play_arrow
question_answer 162) The equation of curve passing through the point\[\left( 1,\frac{\pi }{4} \right)\]and having slope of tangent at any point\[(x,\,\,y)\]as\[\frac{y}{x}-{{\cos }^{2}}\left( \frac{y}{x} \right)\]is
A)
\[x={{e}^{1+\tan \left( \frac{y}{x} \right)}}\]
done
clear
B)
\[x={{e}^{1-\tan \left( \frac{y}{x} \right)}}\]
done
clear
C)
\[x={{e}^{1+\tan \left( \frac{x}{y} \right)}}\]
done
clear
D)
\[x={{e}^{1-\tan \left( \frac{x}{y} \right)}}\]
done
clear
View Answer play_arrow
question_answer 163) If\[P(n):2+4+6+...+(2n),\,\,n\in N\], then\[P(k)=k(k+1)+2\]implies \[P(k+1)=(k+1)(k+2)+2\]is true for all\[k\in N.\] So, statement\[P(n)=n(n+1)+2\]is true for
A)
\[n\ge 1\]
done
clear
B)
\[n\ge 2\]
done
clear
C)
\[n\ge 3\]
done
clear
D)
None of these
done
clear
View Answer play_arrow
question_answer 164) The differential equation of all non-vertical lines in a plane is
A)
\[\frac{{{d}^{2}}y}{d{{x}^{2}}}=0\]
done
clear
B)
\[\frac{{{d}^{2}}x}{d{{y}^{2}}}=0\]
done
clear
C)
\[\frac{dy}{dx}=0\]
done
clear
D)
\[\frac{dx}{dy}=0\]
done
clear
View Answer play_arrow
question_answer 165) The unit vector in ZOX plane and making angle \[{{45}^{o}}\]and \[{{60}^{o}}\]respectively with\[\overset{\to }{\mathop{\mathbf{a}}}\,=2\widehat{\mathbf{i}}+2\widehat{\mathbf{j}}-\widehat{\mathbf{k}}\]and\[\overset{\to }{\mathop{\mathbf{b}}}\,=0\widehat{\mathbf{i}}+\widehat{\mathbf{j}}-\widehat{\mathbf{k}}\], is
A)
\[-\frac{1}{\sqrt{2}}\widehat{\mathbf{i}}+\frac{1}{\sqrt{2}}\widehat{\mathbf{k}}\]
done
clear
B)
\[\frac{1}{\sqrt{2}}\mathbf{\hat{i}}-\frac{1}{\sqrt{2}}\mathbf{\hat{k}}\]
done
clear
C)
\[\frac{1}{3\sqrt{2}}\widehat{\mathbf{i}}+\frac{4}{3\sqrt{2}}\widehat{\mathbf{j}}+\frac{1}{3\sqrt{2}}\widehat{\mathbf{k}}\]
done
clear
D)
None of the above
done
clear
View Answer play_arrow
question_answer 166) If\[\int_{2}^{e}{\left( \frac{1}{\log x}-\frac{1}{{{(\log x)}^{2}}} \right)dx=a+\frac{b}{\log 2}}\],then
A)
\[a=e,\,\,b=-2\]
done
clear
B)
\[a=e,\,\,b=2\]
done
clear
C)
\[a=-e,\,\,b=2\]
done
clear
D)
None of these
done
clear
View Answer play_arrow
question_answer 167) The circle\[{{x}^{2}}+{{y}^{2}}-4x-4y+4=0\]is inscribed in a triangle which has two of its sides along the coordinate axes. If the locus of the circumcentre of the triangle is\[x+y-xy+k\sqrt{{{x}^{2}}+{{y}^{2}}}=0\], then the value of \[k\]is equal to
A)
2
done
clear
B)
1
done
clear
C)
-2
done
clear
D)
3
done
clear
View Answer play_arrow
question_answer 168) The points of discontinuity of tan x are
A)
\[n\pi ,\,\,n\in I\]
done
clear
B)
\[2n\pi ,\,\,n\in I\]
done
clear
C)
\[(2n+1)\frac{\pi }{2},\,\,n\in I\]
done
clear
D)
None of the above
done
clear
View Answer play_arrow
question_answer 169) The two curves\[{{x}^{3}}-3x{{y}^{2}}+2=0\]and\[3{{x}^{2}}y-{{y}^{3}}-2=0\]
A)
cut at right angles
done
clear
B)
touch each other
done
clear
C)
cut at an angle\[\frac{\pi }{3}\]
done
clear
D)
cut at an angle\[\frac{\pi }{4}\]
done
clear
View Answer play_arrow
question_answer 170) The period of the function \[f(x)=\frac{\sin 8x\cos x-\sin 6x\cos 3x}{\cos 2x\cos x-\sin 3x\sin 4x}\]
A)
\[\pi \]
done
clear
B)
\[2\pi \]
done
clear
C)
\[\frac{\pi }{2}\]
done
clear
D)
None of these
done
clear
View Answer play_arrow
question_answer 171) The derivative of\[f(\tan x)\]w.r.t.\[g(\sec x)\]at\[x=\frac{\pi }{4}\], where\[f(1)=2\]and\[g(\sqrt{2})=4\], is
A)
\[\frac{1}{\sqrt{2}}\]
done
clear
B)
\[\sqrt{2}\]
done
clear
C)
1
done
clear
D)
None of these
done
clear
View Answer play_arrow
question_answer 172) If\[a>0,\,\,b>0\]the maximum area of the triangle formed by the points\[O(0,\,\,0)\]\[A(a\cos \theta ,\,\,b\sin \theta )\]and\[B(a\cos \theta ,\,\,-b\sin \theta )\]is (in sq unit)
A)
\[\frac{ab}{2}\]when\[\theta =\frac{\pi }{4}\]
done
clear
B)
\[\frac{3ab}{4}\]when\[\theta =\frac{\pi }{4}\]
done
clear
C)
\[\frac{ab}{2}\]when\[\theta =-\frac{\pi }{2}\]
done
clear
D)
\[{{a}^{2}}{{b}^{2}}\]
done
clear
View Answer play_arrow
question_answer 173) If the two curves \[y={{a}^{x}}\]and\[y={{b}^{x}}\]intersect at an angle\[\alpha \], then tan a equals
A)
\[\frac{\log a-\log b}{1+\log a\log b}\]
done
clear
B)
\[\frac{\log a+\log b}{1-\log a\log b}\]
done
clear
C)
\[\frac{\log a-\log b}{1-\log a\log b}\]
done
clear
D)
None of these
done
clear
View Answer play_arrow
question_answer 174) The number of roots of the equation \[x-\frac{2}{x-1}=1-\frac{2}{x-1}\]
A)
1
done
clear
B)
2
done
clear
C)
0
done
clear
D)
infinitely many
done
clear
View Answer play_arrow
question_answer 175) The vector \[z=-4+5i\]is turned counter clockwise through an angle of\[{{180}^{o}}\]and stretched\[1\frac{1}{2}\]times. The complex number corresponding to newly obtained vector is
A)
\[-6+\frac{15}{2}i\]
done
clear
B)
\[6+\frac{15}{2}i\]
done
clear
C)
\[6-\frac{15}{2}i\]
done
clear
D)
None of these
done
clear
View Answer play_arrow
question_answer 176) If\[A=[{{a}_{ij}}]\]is a4\[4\times 4\]matrix\[{{C}_{ij}}\]is the cofactor of the element\[{{a}_{ij}}\]in\[\left| A \right|\], then the expression\[{{a}_{11}}{{C}_{11}}+{{a}_{12}}{{C}_{12}}+{{a}_{13}}{{C}_{13}}+{{a}_{14}}{{C}_{14}}\]equal to
A)
0
done
clear
B)
-1
done
clear
C)
1
done
clear
D)
\[\left| A \right|\]
done
clear
View Answer play_arrow
question_answer 177) If\[A=\left\{ x:\frac{\pi }{6}\le x\le \frac{\pi }{3} \right\}\]and \[f(x)=\cos x-x(1+x)\], then\[f(A)\]is equal to
A)
\[\left[ -\frac{\pi }{3},\,\,-\frac{\pi }{6} \right]\]
done
clear
B)
\[\left[ \frac{\pi }{6},\,\,\frac{\pi }{3} \right]\]
done
clear
C)
\[\left[ \frac{1}{2}-\frac{\pi }{3}\left( 1+\frac{\pi }{3} \right),\,\,\frac{\sqrt{3}}{2}-\frac{\pi }{6}\left( 1+\frac{\pi }{6} \right) \right]\]
done
clear
D)
\[\left[ \frac{1}{2}+\frac{\pi }{3}\left( 1-\frac{\pi }{3} \right),\,\,\frac{\sqrt{3}}{2}+\frac{\pi }{6}\left( 1-\frac{\pi }{6} \right) \right]\]
done
clear
View Answer play_arrow
question_answer 178) The contrapositive of\[(p\vee q)\Rightarrow r\]is
A)
\[\tilde{\ }r\Rightarrow (p\vee q)\]
done
clear
B)
\[r\Rightarrow (p\vee q)\]
done
clear
C)
\[\tilde{\ }r\Rightarrow (\tilde{\ }p\wedge \tilde{\ }q)\]
done
clear
D)
\[p\Rightarrow (q\vee r)\]
done
clear
View Answer play_arrow
question_answer 179) If the function\[f(x)=a{{x}^{3}}+b{{x}^{2}}+11x-6\]satisfies the condition of Rollers theorem in\[[1,\,\,3]\]and\[f\left( 2+\frac{1}{\sqrt{3}} \right)=0\], then the values of \[a,\text{ }b\]are respectively
A)
- 1, 6
done
clear
B)
- 2, 1
done
clear
C)
1, -6
done
clear
D)
\[-1,\,\,\frac{1}{2}\]
done
clear
View Answer play_arrow
question_answer 180) If\[f(x)=\cos (\log x)\], then \[f\left( \frac{1}{x} \right)f\left( \frac{1}{y} \right)-\frac{1}{2}\left[ f\left( \frac{x}{y} \right)+f(xy) \right]\] is equal to
A)
\[\cos (x-y)\]
done
clear
B)
\[\log (x-y)\]
done
clear
C)
\[\cos (x+y)\]
done
clear
D)
None of these
done
clear
View Answer play_arrow
question_answer 181) If\[\alpha ={{\sin }^{-1}}\frac{\sqrt{3}}{2}+{{\sin }^{-1}}\frac{1}{3}\]and\[\beta ={{\cos }^{-1}}\frac{\sqrt{3}}{2}+{{\cos }^{-1}}\frac{1}{3}\], then
A)
\[\alpha >\beta \]
done
clear
B)
\[\alpha =\beta \]
done
clear
C)
\[\alpha <\beta \]
done
clear
D)
\[\alpha +\beta =2\pi \]
done
clear
View Answer play_arrow
question_answer 182) If\[1+\sin \theta +{{\sin }^{2}}\theta +...\infty =4+2\sqrt{3},\,\,0<\theta <\pi \], \[\theta \ne \frac{\pi }{2}\], then
A)
\[\theta =\frac{\pi }{3}\]
done
clear
B)
\[\theta =\frac{\pi }{6}\]
done
clear
C)
\[\theta =\frac{\pi }{3}\]or\[\frac{\pi }{6}\]
done
clear
D)
\[\theta =\frac{\pi }{3}\]or\[\frac{2\pi }{3}\]
done
clear
View Answer play_arrow
question_answer 183) A round balloon of radius\[r\]subtends an angle \[\alpha \]at the eye of the observer, while the angle of elevation of its centre is\[\beta \]. The height of the centre of balloon is
A)
\[r\cos ec\alpha \sin \frac{\beta }{2}\]
done
clear
B)
\[r\sin \alpha \cos ec\frac{\beta }{2}\]
done
clear
C)
\[r\sin \frac{\alpha }{2}\cos ec\beta \]
done
clear
D)
\[r\cos ec\frac{\alpha }{2}\sin \beta \]
done
clear
View Answer play_arrow
question_answer 184) In\[\Delta ABC,\,\,{{(a-b)}^{2}}{{\cos }^{2}}\frac{C}{2}+{{(a+b)}^{2}}{{\sin }^{2}}\frac{C}{2}\]is equal to
A)
\[{{a}^{2}}\]
done
clear
B)
\[{{b}^{2}}\]
done
clear
C)
\[{{c}^{2}}\]
done
clear
D)
None of these
done
clear
View Answer play_arrow
question_answer 185) In a triangle\[\left( 1-\frac{{{r}_{1}}}{{{r}_{2}}} \right)\left( 1-\frac{{{r}_{1}}}{{{r}_{2}}} \right)=2\], then the triangle is
A)
right angled
done
clear
B)
isosceles
done
clear
C)
equilateral
done
clear
D)
None of these
done
clear
View Answer play_arrow
question_answer 186) If\[a+b+c=0\], then the roots of the equation \[4a{{x}^{2}}+3bx+2c=0\]are
A)
equal
done
clear
B)
imaginary
done
clear
C)
real
done
clear
D)
None of these
done
clear
View Answer play_arrow
question_answer 187)
The adjoining graph
A)
Connected
done
clear
B)
Disconnected
done
clear
C)
Neither connected nor disconnected
done
clear
D)
None of the above
done
clear
View Answer play_arrow
question_answer 188) The solution of\[{{\tan }^{-1}}x+2{{\cot }^{-1}}x=\frac{2\pi }{3}\]is
A)
\[-\frac{1}{\sqrt{3}}\]
done
clear
B)
\[\frac{1}{\sqrt{3}}\]
done
clear
C)
\[-\sqrt{3}\]
done
clear
D)
\[\sqrt{3}\]
done
clear
View Answer play_arrow
question_answer 189) The conjugate of the complex number\[\frac{{{(1+i)}^{2}}}{1-i}\]is
A)
\[1-i\]
done
clear
B)
\[1+i\]
done
clear
C)
\[-1+i\]
done
clear
D)
\[-1-i\]
done
clear
View Answer play_arrow
question_answer 190) A graph\[G\]has\[m\]vertices of odd degree and \[n\]vertices of even degree. Then which of the following statements is necessarily true?
A)
\[m+n\]is an odd number
done
clear
B)
\[m+n\]is an even number
done
clear
C)
\[n+1\]is an even number
done
clear
D)
\[m+1\]is an odd number
done
clear
View Answer play_arrow
question_answer 191) The value of\[\sin \left[ 2{{\cos }^{-1}}\frac{\sqrt{5}}{3} \right]\]is
A)
\[\frac{\sqrt{5}}{3}\]
done
clear
B)
\[\frac{2\sqrt{5}}{3}\]
done
clear
C)
\[\frac{4\sqrt{5}}{9}\]
done
clear
D)
\[\frac{2\sqrt{5}}{9}\]
done
clear
View Answer play_arrow
question_answer 192) In the group\[(G,{{\otimes }_{15}})\], where\[G=\{3,\,\,6,\,\,9,\,\,12\}\], \[{{\otimes }_{15}}\]is multiplication modulo 15, the identity element is
A)
3
done
clear
B)
6
done
clear
C)
12
done
clear
D)
9
done
clear
View Answer play_arrow
question_answer 193) A group\[(G,\,\,*)\]has 10 elements. The minimum number of elements of\[G\], which are their own inverses is
A)
2
done
clear
B)
1
done
clear
C)
9
done
clear
D)
0
done
clear
View Answer play_arrow
question_answer 194) \[\frac{3{{x}^{2}}+1}{{{x}^{2}}-6x+8}\]is equal to
A)
\[3+\frac{49}{2(x-4)}-\frac{13}{2(x-2)}\]
done
clear
B)
\[\frac{49}{2(x-4)}-\frac{13}{2(x-2)}\]
done
clear
C)
\[\frac{-49}{2(x-4)}+\frac{13}{2(x-2)}\]
done
clear
D)
\[\frac{49}{2(x-4)}+\frac{13}{2(x-2)}\]
done
clear
View Answer play_arrow
question_answer 195) The orthocentre of the triangle with vertices\[O(0,\,\,0),\,\,A\left( 0,\,\,\frac{3}{2} \right),\,\,B(-5,\,\,0)\]is
A)
\[\left( \frac{5}{2},\,\,\frac{3}{4} \right)\]
done
clear
B)
\[\left( \frac{-5}{2},\,\,\frac{3}{4} \right)\]
done
clear
C)
\[\left( -5,\,\,\frac{3}{2} \right)\]
done
clear
D)
\[(0,\,\,0)\]
done
clear
View Answer play_arrow
question_answer 196) The range in which\[y=-{{x}^{2}}+6x-3\]increasing, is
A)
\[x<3\]
done
clear
B)
\[x>3\]
done
clear
C)
\[7<x<8\]
done
clear
D)
\[5<x<6\]
done
clear
View Answer play_arrow
question_answer 197) The area bounded by the curve\[x=4-{{y}^{2}}\]and the y-axis is
A)
16 sq unit
done
clear
B)
32 sq unit
done
clear
C)
\[\frac{32}{3}\]sq unit
done
clear
D)
\[\frac{16}{3}\]sq unit
done
clear
View Answer play_arrow
question_answer 198) The number of positive divisors of 252 is
A)
9
done
clear
B)
5
done
clear
C)
18
done
clear
D)
10
done
clear
View Answer play_arrow
question_answer 199) The remainder obtained when 5124 is divided by 124 is
A)
5
done
clear
B)
0
done
clear
C)
2
done
clear
D)
1
done
clear
View Answer play_arrow
question_answer 200) Which of the following is not a group with respect to the given operation?
A)
The set of even integers including zero under addition
done
clear
B)
The set of odd integers under addition
done
clear
C)
{0} under addition
done
clear
D)
{1,-1} under multiplication
done
clear
View Answer play_arrow
question_answer 201) He is so ...... of his own idea that he will not entertain any suggestion from others.
A)
hopeful
done
clear
B)
enamoured
done
clear
C)
jealous
done
clear
D)
possessed
done
clear
View Answer play_arrow
question_answer 202) Undoubtedly, English is the most...... spoken language in the world today.
A)
broadly
done
clear
B)
widely
done
clear
C)
greatly
done
clear
D)
beautifully
done
clear
View Answer play_arrow
question_answer 203) I will be leaving for Delhi tonight and ...... to return by this weekend.
A)
waiting
done
clear
B)
plan
done
clear
C)
going
done
clear
D)
making
done
clear
View Answer play_arrow
question_answer 204) The vacancy ......... by the dismissal of the superintendent is expected to be filled up by the promotion of a U.D.C.
A)
made
done
clear
B)
created
done
clear
C)
caused
done
clear
D)
generated
done
clear
View Answer play_arrow
question_answer 205) HAGGLE
A)
Postpone
done
clear
B)
Accept
done
clear
C)
Bargain
done
clear
D)
Reject
done
clear
View Answer play_arrow
question_answer 206) ABSTRUSE
A)
Awful
done
clear
B)
Irrelevant
done
clear
C)
Shallow
done
clear
D)
Profound
done
clear
View Answer play_arrow
question_answer 207) PENCHANT
A)
Like
done
clear
B)
Eagerness
done
clear
C)
Disability
done
clear
D)
Dislike
done
clear
View Answer play_arrow
question_answer 208) BARTER
A)
Deal
done
clear
B)
Return
done
clear
C)
Lend
done
clear
D)
Exchange
done
clear
View Answer play_arrow
question_answer 209) Bringing about gentle and painless death from incurable disease
A)
Gallows
done
clear
B)
Suicide
done
clear
C)
Euphoria
done
clear
D)
Euthanasia
done
clear
View Answer play_arrow
question_answer 210) The act of killing ones wife
A)
Avicide
done
clear
B)
Canicide
done
clear
C)
Uxoricide
done
clear
D)
Genocide
done
clear
View Answer play_arrow
question_answer 211) Stage between boyhood and youth
A)
Infancy
done
clear
B)
Adolescence
done
clear
C)
Puberty
done
clear
D)
Maturity
done
clear
View Answer play_arrow
question_answer 212) Lack of enough blood
A)
Amnesia
done
clear
B)
Insomnia
done
clear
C)
Anaemia
done
clear
D)
Allergy
done
clear
View Answer play_arrow
question_answer 213) To set the people by ears
A)
To box the people
done
clear
B)
To insult and disgrace the people
done
clear
C)
To punish heavily
done
clear
D)
To excite people to a quarrel
done
clear
View Answer play_arrow
question_answer 214) To give chapter and verse for a thing
A)
To produce the proof of something
done
clear
B)
To eulogise the qualities of a thing
done
clear
C)
To make publicity of a thing
done
clear
D)
To attach artificial value to a thing
done
clear
View Answer play_arrow
question_answer 215) Dog in the manger
A)
An undersized bull almost the shape of a dog
done
clear
B)
A dog that has no kennel of its own
done
clear
C)
A person who puts himself in difficulties an account of other people
done
clear
D)
A person who prevents others from enjoying something useless to himself
done
clear
View Answer play_arrow
question_answer 216) To blow hot and cold
A)
Changing weather
done
clear
B)
To be untrustworthy
done
clear
C)
To change opinion often
done
clear
D)
To be rich and poor frequently
done
clear
View Answer play_arrow
question_answer 217) SAGACIOUS
A)
Casual
done
clear
B)
Cunning
done
clear
C)
Foolish
done
clear
D)
False
done
clear
View Answer play_arrow
question_answer 218) EPILOGUE
A)
Conversation
done
clear
B)
Dialogue
done
clear
C)
Dramatic
done
clear
D)
Prologue
done
clear
View Answer play_arrow
question_answer 219) AUSPICIOUS
A)
Spicy
done
clear
B)
Unfavorable
done
clear
C)
Conspicuous
done
clear
D)
Condemnatory
done
clear
View Answer play_arrow
question_answer 220) ENGULFED
A)
Encircled
done
clear
B)
Groped
done
clear
C)
Disfigured
done
clear
D)
Detached
done
clear
View Answer play_arrow
question_answer 221) Four of the following five are alike in a certain way and so form a group. Which is the one that does not belong to that group?
A)
Hill
done
clear
B)
Valley
done
clear
C)
Dam
done
clear
D)
River
done
clear
View Answer play_arrow
question_answer 222) In a certain code CREAM is written as NBDBQ. How in BREAD written in that code?
A)
EBFAQ
done
clear
B)
EBDAQ
done
clear
C)
BEDQA
done
clear
D)
BEFQA
done
clear
View Answer play_arrow
question_answer 223) If black means white, white means red, red means yellow, yellow means blue, blue means green, green means purple and purple means orange, then what is the colour of lemon?
A)
Green
done
clear
B)
Purple
done
clear
C)
Orange
done
clear
D)
Blue
done
clear
View Answer play_arrow
question_answer 224) Directions: In the following questions, find the word which holds the same relation with the third word as there in between the first two word. Hot: Oven : : Cold :?
A)
Ice cream
done
clear
B)
Air conditioner
done
clear
C)
Snow
done
clear
D)
Refrigerator
done
clear
View Answer play_arrow
question_answer 225) Directions: In the following questions, find the word which holds the same relation with the third word as there in between the first two word. Push : Pull : : Throw :?
A)
Jump
done
clear
B)
Collect
done
clear
C)
Pick
done
clear
D)
Game
done
clear
View Answer play_arrow
question_answer 226) Directions: In each of the following questions, one letter or a set of letter is missing, you have to understand the pattern of the series and insert the appropriate letter? R, M, ?, F, D, ?
A)
C, B
done
clear
B)
J, H
done
clear
C)
H, C
done
clear
D)
I, C
done
clear
View Answer play_arrow
question_answer 227) Directions: In each of the following questions, one letter or a set of letter is missing, you have to understand the pattern of the series and insert the appropriate letter? - bcc - ac - aabb - ab -cc
A)
aab ca
done
clear
B)
aba ca
done
clear
C)
ba cab
done
clear
D)
bca ca.
done
clear
View Answer play_arrow
question_answer 228) How many 9s are there in the following number series which are immediately preceded by 3 and followed by 6? 3 9 6 9 3 9 3 9 3 9 6 3 9 3 6 3 9 5 6 9 5 6 9 3 9 6 3 9
A)
0
done
clear
B)
3
done
clear
C)
2
done
clear
D)
4
done
clear
View Answer play_arrow
question_answer 229) Some boys are sitting in a row, P in sitting fourteenth from the left and Q is seventh from the right. If these are four boys between P and Q, how many boys are there in the row?
A)
25
done
clear
B)
23
done
clear
C)
21
done
clear
D)
19
done
clear
View Answer play_arrow
question_answer 230) Pointing to a photograph, a woman says, this mans sons sister in my mother-in-law. How is the womans husband related to the man in the photograph?
A)
Grandson
done
clear
B)
Son
done
clear
C)
Son-in-law
done
clear
D)
Nephew
done
clear
View Answer play_arrow
question_answer 231) The longest canal in the world is
A)
Volga Baltic
done
clear
B)
Beloye-more Baltic
done
clear
C)
Suez Canal
done
clear
D)
Grand China Canal
done
clear
View Answer play_arrow
question_answer 232) The oldest Hindu epic is
A)
Mahabhashya
done
clear
B)
Ramayan
done
clear
C)
Mahabharata
done
clear
D)
Ashtadhyayi
done
clear
View Answer play_arrow
question_answer 233) Who among the following is not associated with the Swaraj Party?
A)
C.R. Das
done
clear
B)
M.L. Kelkar
done
clear
C)
Motilal Nehru
done
clear
D)
Mahatma Gandhi
done
clear
View Answer play_arrow
question_answer 234) Where is the City of palaces?
A)
London
done
clear
B)
Kolkata
done
clear
C)
Patiala
done
clear
D)
Lucknow
done
clear
View Answer play_arrow
question_answer 235) Our National Song is
A)
Sare Jahan Se Achcha
done
clear
B)
Jana Gana Mana
done
clear
C)
Vande Mataram
done
clear
D)
All of the above
done
clear
View Answer play_arrow
question_answer 236) The Constitution of India was adopted by the Constituent Assembly on
A)
Dec 11, 1946
done
clear
B)
Aug 15, 1957
done
clear
C)
Nov 26, 1949
done
clear
D)
Jan 26, 1949
done
clear
View Answer play_arrow
question_answer 237) Gandhijis Dandi March started from
A)
Bardoli
done
clear
B)
Ahmedabad
done
clear
C)
Surat
done
clear
D)
Bombay
done
clear
View Answer play_arrow
question_answer 238) Who was the viceroy of India at the time of formation of the Indian National Congress?
A)
Lord Canning
done
clear
B)
Lord Dufferin
done
clear
C)
Lord Mayo
done
clear
D)
Lord Elgin
done
clear
View Answer play_arrow
question_answer 239) Which country was a major donor in financing the SAARC?
A)
Pakistan
done
clear
B)
Sri Lanka
done
clear
C)
India
done
clear
D)
Bangladesh
done
clear
View Answer play_arrow
question_answer 240) Where in the H. Q. of the European Economic Community?
A)
Bonn
done
clear
B)
Rome
done
clear
C)
Brussels
done
clear
D)
Hague
done
clear
View Answer play_arrow