question_answer

If the tangent to ellipse\[{{x}^{2}}+2y=1\]at point \[P\left( \frac{1}{\sqrt{2}},\,\,\frac{1}{2} \right)\] meets the auxiliary circle at the points\[R\]and\[Q\], then tangents to circle at\[Q\]and\[R\]intersect at

A) \[\left( \frac{1}{\sqrt{2}},\,\,1 \right)\]                 

B) \[\left( 1,\,\,\frac{1}{\sqrt{2}} \right)\]

C) \[\left( \frac{1}{2},\,\,\frac{1}{2} \right)\]            

D)        \[\left( \frac{1}{2},\,\,\frac{1}{\sqrt{2}} \right)\]

Correct Answer: A

Solution :

Equation of tangent to ellipse at given point is                 \[x\left( \frac{1}{\sqrt{2}} \right)+2y\left( \frac{1}{2} \right)=1\] \[\Rightarrow \]               \[x+\sqrt{2}y=\sqrt{2}\]                                               ? (i)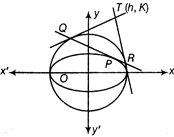 Now,\[QR\]is chord of contact of circle\[{{x}^{2}}+{{y}^{2}}=1\]with respect to point\[T(h,\,\,K)\]. then,                     \[QR\equiv hx+Ky=1\]   ... (ii) Equations (I) and (Ii) represent same straight line, then comparing ratio of coefficients we have                 \[\frac{h}{1}=\frac{K}{\sqrt{2}}=\frac{1}{\sqrt{2}}\] Hence;\[(h,\,\,K)\equiv \left( \frac{1}{\sqrt{2}},\,\,1 \right)\]