question_answer

The parabola\[{{y}^{2}}=x\] divides the circle \[{{x}^{2}}+{{y}^{2}}=2\]into two parts whose areas are in the ratio   JEE Main Online Paper (Held On 07 May 2012)

A) \[9\pi +2:3\pi -2\]           

B)                        \[9\pi -2:3\pi +2\]

C)                        \[7\pi -2:2\pi -3\]            

D)                        \[7\pi +2:3\pi +2\]

Correct Answer: B

Solution :

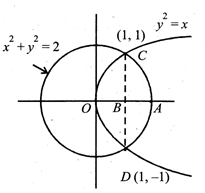                Area of circle\[\pi ={{\left( \sqrt{2} \right)}^{2}}=2\pi \] Area of OCADO =2 {Area of OCAO} = 2 {area of OCB + area of BCA} \[=2\int\limits_{0}^{1}{{{y}_{p}}dx+2}\int\limits_{1}^{\sqrt{2}}{{{y}_{c}}dx}\]where\[{{y}_{p}}=\sqrt{x}\]and\[{{y}_{c}}=\sqrt{2-{{x}^{2}}}\] \[\therefore \]Required Area\[=2\int\limits_{0}^{1}{\sqrt{x}\,dx+2}\int\limits_{1}^{\sqrt{2}}{\sqrt{2-{{x}^{2}}}}dx\] \[=2\left[ \frac{2}{3}.1-0 \right]+2\left[ \frac{x\sqrt{2-{{x}^{2}}}}{2}+{{\sin }^{-1}}\frac{x}{\sqrt{2}} \right]_{1}^{\sqrt{2}}\] \[=\frac{4}{3}+2\left\{ \frac{\pi }{2}-\frac{\pi }{4}-\frac{1}{2} \right\}=\frac{4}{3}+2\left\{ \frac{\pi }{4}-\frac{1}{2} \right\}=\frac{3\pi +2}{6}\] \[\therefore \]Required Ratio \[=\frac{9\pi -2}{3\pi +2}\]i.e.,\[9\pi -2:3\pi +2\]