A) \[8\sqrt{3}\pi \]
B) \[6\sqrt{2}\pi \]
C) \[6\sqrt{3}\pi \]
D) \[8\sqrt{2}\pi \]
Correct Answer: A
Solution :
Sphere of radius :\[3cm(r=3)\] Let \[b,h\] be radius and height of sphere, respectively. \[\therefore \] volume of cone\[=\frac{1}{3}\pi {{b}^{2}}h\] In \[\Delta ABC\], using Pythagoras theorem \[{{(h-r)}^{2}}+{{b}^{2}}={{r}^{2}}........(i)\] \[{{b}^{2}}={{r}^{2}}-{{(h-r)}^{2}}={{r}^{2}}-({{h}^{2}}-2hr+{{r}^{2}})=2hr-{{h}^{2}}\] \[\therefore \] volume \[v=\frac{1}{3}h[{{r}^{2}}-{{(h-r)}^{2}}]\] \[=\frac{1}{3}\pi h[2hr-{{h}^{2}}]=\frac{1}{3}[2{{h}^{2}}r-{{h}^{3}}]\] \[\frac{dv}{dh}=\frac{1}{3}[4hr-3{{h}^{2}}]=0\Rightarrow h(4r-3h)=0\] \[\frac{{{d}^{2}}v}{d{{h}^{2}}}=\frac{1}{3}[4r-6h]\] At \[h=\frac{4r}{3},\frac{{{d}^{2}}v}{d{{h}^{2}}}=\frac{1}{3}[4r-\frac{4r}{3}\times 6]\] \[=\frac{1}{3}[4r-8r]<0\Rightarrow \]maximum volume at \[h=\frac{4r}{3}\] \[h=\frac{4r}{3}=4\] \[\therefore \] From (1) \[{{(h-r)}^{2}}+{{b}^{2}}={{r}^{2}}\] \[\Rightarrow {{b}^{2}}=2hr-{{h}^{2}}\] \[=2\cdot \frac{4r}{3}r-\frac{16{{r}^{2}}}{9}\] \[=\frac{8{{r}^{2}}}{3}-\frac{16{{r}^{2}}}{9}\] \[=\frac{{{(24-16)}^{{{r}^{2}}}}}{9}=\frac{8{{r}^{2}}}{9}\] \[=b=\frac{2\sqrt{2}}{3}r\Rightarrow 2\sqrt{2}\] Curved surface area \[=\pi bl\] \[=\pi b\sqrt{{{h}^{2}}+{{r}^{2}}}\] \[=\pi 2\sqrt{2}\sqrt{{{4}^{2}}+8}\] \[=\pi 2\sqrt{2}\sqrt{24}\] \[=\pi 2\sqrt{22}\sqrt{3}\sqrt{2}\] \[=8\sqrt{3}\pi \].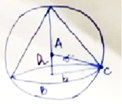
You need to login to perform this action.
You will be redirected in
3 sec
