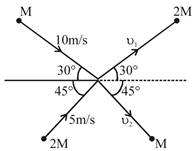
[JEE Main 10-4-2019 Morning]
A) 3.2 m/s and 6.3 m/s
B) 3.2 m/s and 12.6 m/s
C) 6.5 m/s and 6.3 m/s
D) 6.5 m/s and 3.2 m/s
Correct Answer: C
Solution :
\[M\times 10\cos {{30}^{o}}+2M\times 5\cos {{45}^{o}}\] \[=2M\times {{\text{v}}_{1}}\cos {{30}^{o}}+M\,{{\text{v}}_{2}}\cos {{45}^{o}}\] \[5\sqrt{3}+5\sqrt{2}=2{{\text{v}}_{1}}\frac{\sqrt{3}}{2}+\frac{{{\text{v}}_{2}}}{\sqrt{2}}\] \[10\times \text{ }M\text{ sin }30{}^\circ 2M\times 5\text{ sin }45{}^\circ \] \[=M\text{ }{{\text{v}}_{2}}\text{ sin }45{}^\circ 2M\text{ }{{\text{v}}_{1}}\text{ sin }30{}^\circ \] \[5-5\sqrt{2}=\frac{{{\text{v}}_{2}}}{\sqrt{2}}-{{\text{v}}_{1}}\] Solving \[{{\text{v}}_{1}}=\frac{17.5}{2.7}\simeq 6.5m/s\] \[{{\text{v}}_{2}}\approx 6.3\,m/s\]
You need to login to perform this action.
You will be redirected in
3 sec
