question_answer

If one end of a focal chord of the parabola, \[{{y}^{2}}=16x\] is at (1, 4), then the length of this focal chord is [JEE Main 9-4-2019 Morning]

A) 25       

B) 24

C) 20                               

D) 22

Correct Answer: A

Solution :

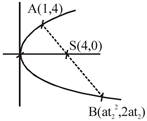\[{{y}^{2}}=4ax=16x\Rightarrow a=4\] \[A(1,4)\Rightarrow 2.4{{t}_{1}}=4\Rightarrow {{t}_{1}}=\frac{1}{2}\] \[\therefore \] length of focal chord\[=a{{\left( t+\frac{1}{t} \right)}^{2}}\] \[=4{{\left( \frac{1}{2}+2 \right)}^{2}}=4.\frac{25}{4}=25\]