question_answer

If a tangent to the circle\[{{x}^{2}}+{{y}^{2}}=1\]intersects the coordinate axes at distinct points P and Q, then the locus of the mid-point of PQ is [JEE Main 9-4-2019 Morning]

A) \[{{x}^{2}}+{{y}^{2}}2xy=0\]

B) \[{{x}^{2}}+{{y}^{2}}16{{x}^{2}}{{y}^{2}}=0\]

C) \[{{x}^{2}}+{{y}^{2}}4{{x}^{2}}{{y}^{2}}=0\]

D) \[{{x}^{2}}+{{y}^{2}}2{{x}^{2}}{{y}^{2}}=0\]

Correct Answer: C

Solution :

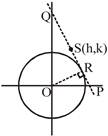Let the mid point be S(h,k) \[\therefore \]P(2h,0) and Q(0,2k) equation of  \[PQ:\frac{x}{2h}+\frac{y}{2k}=1\] \[\because PQ\]is tangent to circle at R(say) \[\therefore \] 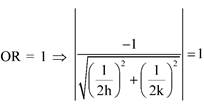\[\Rightarrow \frac{1}{4{{h}^{2}}}+\frac{1}{4{{k}^{2}}}=1\] \[\Rightarrow {{x}^{2}}+{{y}^{2}}-4{{x}^{2}}{{y}^{2}}=0\] Aliter : tangent to circle \[x\cos \theta +y\sin \theta =1\] \[P:(sec\theta ,0)\] \[Q:(0,cosec\theta )\] \[2h=\sec \theta \Rightarrow \cos \theta =\frac{1}{2h}\And \sin \theta =\frac{1}{2k}\] \[\frac{1}{{{\left( 2x \right)}^{2}}}+\frac{1}{{{\left( 2y \right)}^{2}}}=1\]