question_answer

Following figure shows two processes A and B for a gas. If \[\Delta {{Q}_{A}}\]and \[\Delta {{Q}_{B}}\]are the amount of heat absorbed by the system in two cases, and \[\Delta {{U}_{A}}\]and \[\Delta {{U}_{B}}\]are changes in internal energies, respectively, then : [JEE Main 9-4-2019 Morning]

A) \[\Delta {{Q}_{A}}=\Delta {{Q}_{B}};\Delta {{U}_{A}}=\Delta {{U}_{B}}\]

B) \[\Delta {{Q}_{A}}>\Delta {{Q}_{B}};\Delta {{U}_{A}}=\Delta {{U}_{B}}\]

C) \[\Delta {{Q}_{A}}>\Delta {{Q}_{B}};\Delta {{U}_{A}}>\Delta {{U}_{B}}\]

D) \[\Delta {{Q}_{A}}<\Delta {{Q}_{B}};\Delta {{U}_{A}}<\Delta {{U}_{B}}\]

Correct Answer: B

Solution :

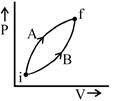
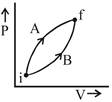Initial and final states for both the processes are same. \[\therefore \]\[\Delta {{U}_{A}}=\Delta {{U}_{B}}\] Work done during process A is greater than in process B. By First Law of thermodynamics \[\Delta Q=\Delta U+W\]\[\Rightarrow \]\[\Delta {{Q}_{A}}>\Delta {{Q}_{B}}\]