question_answer

                A tangent to the hyperbola \[\frac{{{x}^{2}}}{4}-\frac{{{y}^{2}}}{2}=1\] meets \[x-\]axis at P and \[y-\]axis at \[Q.\]Lines PR and QR are drawn such that OPRQ is a rectangle (where O is the origin). The R lies on:     JEE Main Online Paper ( Held On 23  April 2013 )

A)                  ­\[\frac{4}{{{x}^{2}}}+\frac{2}{{{y}^{2}}}=1\]                       

B)                                         \[\frac{2}{{{x}^{2}}}-\frac{4}{{{y}^{2}}}=1\]

C)                                         \[\frac{2}{{{x}^{2}}}+\frac{4}{{{y}^{2}}}=1\]                       

D)                                         \[\frac{4}{{{x}^{2}}}-\frac{2}{{{y}^{2}}}=1\]

Correct Answer: D

Solution :

                  Equation of the tangent at the point '\[\theta \]' is \[\frac{x\sec \theta }{a}-\frac{y\tan \theta }{b}=1\] \[\Rightarrow \]\[P=(a\cos \theta ,0)\]and\[Q=(0,-b\cot \theta )\] Let R be\[(h,k)\Rightarrow h=a\cos \theta ,k=-b\cot \theta \] \[\Rightarrow \]\[\frac{k}{h}=\frac{-b}{a\sin \theta }\Rightarrow \sin \theta =\frac{-bh}{ak}\]and\[\cos \theta =\frac{h}{a}\] By squaring and adding,\[\frac{{{b}^{2}}{{h}^{2}}}{{{a}^{2}}{{k}^{2}}}+\frac{{{h}^{2}}}{{{a}^{2}}}=1\]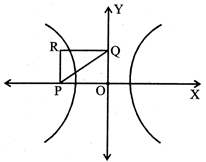 \[\Rightarrow \]\[\frac{{{b}^{2}}}{{{k}^{2}}}+1=\frac{{{a}^{2}}}{{{h}^{2}}}\]\[\Rightarrow \]\[\frac{{{a}^{2}}}{{{h}^{2}}}-\frac{{{b}^{2}}}{{{k}^{2}}}=1\] Now, given \[e{{q}^{n}}\]of hyperbola is \[\frac{{{x}^{2}}}{4}-\frac{{{y}^{2}}}{2}=1\]\[\Rightarrow \]\[{{a}^{2}}=4,{{b}^{2}}=2\] \[\therefore \]R lies on \[\frac{{{a}^{2}}}{{{x}^{2}}}-\frac{{{b}^{2}}}{{{y}^{2}}}=1\]i.e.,\[\frac{4}{{{x}^{2}}}-\frac{2}{{{y}^{2}}}=1\]