question_answer

Let \[0<\theta <\frac{\pi }{2}\]. If the eccentricity of the hyperbola \[\frac{{{x}^{2}}}{{{\cos }^{2}}\theta }-\frac{{{y}^{2}}}{{{\sin }^{2}}\,\theta }\,\,=\,\,1\] is greater than 2, then the length of its latus rectum   lies in the interval: [JEE Main Online Paper (Held On 09-Jan-2019 Morning]

A) \[\left( 3,\text{ }\infty  \right)\]

B) (1, 3/2]

C) (3/2, 2]

D) (2, 3]

Correct Answer: A

Solution :

\[si{{n}^{2}}\,\theta \,\,=\,\,co{{s}^{2}}\theta \,\,({{e}^{2}}\,-1)\] \[{{\tan }^{2}}\,\theta \,\,=\,\,{{e}^{2}}\,\,-1\] \[1\text{ }+\text{ }ta{{n}^{2}}\theta \text{ }=\text{ }{{e}^{2}}\]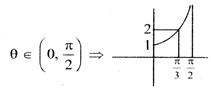 \[e\,\,=\,\,\sqrt{{{\sec }^{2}}\,\theta }\] \[e\,\,=\,\,sec\,\theta \] \[\sec \,\,\theta \,\,>\,\,2\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\Rightarrow \,\,\frac{1}{\cos \,\theta }\,\,>\,\,2\] \[\theta \,\in \,\,\left( \frac{\pi }{3},\,\,\frac{\pi }{2} \right)\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,0\,\,<\,\,\cos \,\theta \,\,\,<\,\,sss\,\,\frac{1}{2}\,\] length of LR \[=\,\,\frac{2{{b}^{2}}}{a}\,\,\,=\,\,\frac{2.{{\sin }^{2}}\,\theta }{\cos \,\theta }\,\,\] = \[\frac{2(1-co{{s}^{2}}\theta )}{\cos \,\theta }\] \[\,\left( \frac{\pi }{3},\,\,\,\frac{\pi }{2} \right)\,\,\uparrow \,\,function\] min exist at \[\theta \,\,\,=\,\,\frac{\pi }{3}\] max exist at \[\theta \,\,\,=\,\,\frac{\pi }{2}\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\Rightarrow \,\,(3,\,\,\,\infty )\]