question_answer

    One root of the equation\[\left| \begin{matrix}    x+a & b & c  \\    b & x+c & a  \\    c & a & x+b  \\ \end{matrix} \right|=0\]is

A)  \[-(a+b)\]                          

B)  \[-(b+c)\]

C)  \[-a\]                                   

D)  \[-(a+b+c)\]

Correct Answer: D

Solution :

                Let\[p(at_{1}^{2},2a{{t}_{1}})\]and \[Q(at_{2}^{2},2a{{t}_{2}})\]be the end points of the focal chord PQ  of the parabola \[{{y}^{2}}=4ax\]and which makes an angle\[\alpha \]with the axis of parabola.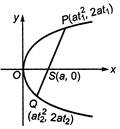 Now, \[PQ=\sqrt{{{(at_{2}^{2}-at_{1}^{2})}^{2}}+{{(2a{{t}_{2}}-2a{{t}_{1}})}^{2}}}\] \[=a\sqrt{{{(t_{2}^{2}-t_{1}^{2})}^{2}}+4{{({{t}_{2}}-{{t}_{1}})}^{2}}}\] \[=a\sqrt{{{({{t}_{2}}+{{t}_{1}})}^{2}}{{({{t}_{2}}-{{t}_{1}})}^{2}}+4{{({{t}_{2}}-{{t}_{1}})}^{2}}}\] \[=a({{t}_{2}}-{{t}_{1}})\sqrt{t_{2}^{2}+t_{1}^{2}+2{{t}_{1}}{{t}_{2}}+4}\] \[=a({{t}_{2}}-{{t}_{1}})\sqrt{t_{2}^{2}+t_{1}^{2}-2+4}\]                \[(\because {{t}_{1}}{{t}_{2}}=-1)\] \[=a({{t}_{2}}-{{t}_{1}})\sqrt{t_{2}^{2}+t_{1}^{2}+2}\] \[=a({{t}_{2}}-{{t}_{1}})\sqrt{(t_{2}^{2}+t_{1}^{2}-2{{t}_{1}}{{t}_{2}})}\]                \[(\because {{t}_{1}}{{t}_{2}}=-1)\] \[PQ=a({{t}_{2}}-{{t}_{1}})\sqrt{{{({{t}_{2}}-{{t}_{1}})}^{2}}}\] \[=a{{({{t}_{2}}-{{t}_{1}})}^{2}}\] and slope of\[PQ=\frac{2a{{t}_{2}}-2a{{t}_{1}}}{at_{2}^{2}-at_{1}^{2}}\] \[\tan \alpha =\frac{2a({{t}_{2}}-{{t}_{1}})}{a({{t}_{2}}-{{t}_{1}})({{t}_{2}}-{{t}_{1}})}\] \[\Rightarrow \]               \[\tan \alpha =\frac{2}{{{t}_{1}}+{{t}_{2}}}\] \[\Rightarrow \]               \[2\cot \alpha ={{t}_{1}}+{{t}_{2}}\] Again, we have Eq. (i) \[PQ=a{{({{t}_{2}}-{{t}_{1}})}^{2}}\] \[=a[{{({{t}_{2}}+{{t}_{1}})}^{2}}-4{{t}_{1}}{{t}_{2}}]\] \[=a[{{(2\cot \alpha )}^{2}}+4]\]                      \[[\because {{t}_{1}}+{{t}_{2}}=2\cot \alpha \,\,and\,{{t}_{1}}{{t}_{2}}=-1]\] \[=4a(1+{{\cot }^{2}}\alpha )\] \[PQ=4a\,\cos e{{c}^{2}}\alpha \]