question_answer

\[f(x)=\left\{ \begin{matrix}    2a-x & in & -a<x<a  \\    3x-2a & in & a\le x  \\ \end{matrix} \right.\] Then, which of the following is true?

A)  \[f(x)\] is discontinuous at \[x=a\]

B)  \[f(x)\] is not differentiable at \[x=a\]

C)  \[f(x)\] is differentiable at \[x\ge a\]

D)  \[f(x)\] is continuous at all \[x<a\]

Correct Answer: B

Solution :

Given,    \[f(x)=\left\{ \begin{matrix}    2a-x & in & -a<x<a  \\    3x-2a & in & a\le x  \\ \end{matrix} \right.\] At \[x=a\] LHL= \[\underset{x\to {{a}^{-}}}{\mathop{\lim }}\,f(x)\]                 \[=\underset{x\to a}{\mathop{\lim }}\,\,2a-x=a\] RHL \[=\underset{x\to {{a}^{+}}}{\mathop{\lim }}\,f(x)\]                 \[=\underset{x\to a}{\mathop{\lim }}\,\,3x-2a=a\] and        \[f(a)=3(a)-2a=a\] \[\therefore \] LHL = RHL =\[f(a)\] Hence, it is continuous at \[x=a\] Again, at \[x=a\] LHD \[=\underset{h\to 0}{\mathop{lim}}\,\frac{f(a-h)-f(a)}{-h}\]                 \[=\underset{h\to 0}{\mathop{lim}}\,\frac{2a-(a-h)-a}{-h}=\frac{h}{-h}=-1\] and RHD  \[=\underset{h\to 0}{\mathop{\lim }}\,\frac{f(a+h)-f(a)}{h}\]                 \[=\underset{h\to 0}{\mathop{\lim }}\,\frac{3(a+h)-2a-a}{h}=3\] \[\therefore \]  \[LHD\ne RHD\] Hence, it is not differentiable at \[x=a\]. Alternate Solution Let \[y=f(x)=\left\{ \begin{matrix}    2a-x & in & -a<x<a  \\    3x-2a & in & a\le x  \\ \end{matrix} \right.\]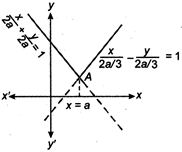                 It is clear from the graph that \[f(x)\] is continuous everywhere it is also differentiable everywhere except a point A at \[x=a\]