question_answer

The line \[x+y=a\]meets the axes of X and Y at A and B respectively. \[A\Delta AMN\]is inscribed in the \[\text{ }\!\!\Delta\!\!\text{ }\,\text{O}\,\text{A}\,\text{B,}\] O being the origin, with right angle at N. M and N lie on OB and AB respectively. If the area of the \[\Delta AMN\]is \[\frac{3}{8}\] of the area of the \[\Delta OAB,\] then\[\frac{AN}{BN}\] is equal to

A)  \[\frac{1}{3}\]                  

B) \[\frac{1}{3},3\]                              

C) \[\frac{2}{3},3\]                              

D) \[3\]

Correct Answer: D

Solution :

Let \[\frac{AN}{B\lambda }=\lambda \]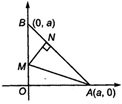 then by section formula, the coordinates of N are                                 \[\left( \frac{a}{1+\lambda },\frac{\lambda a}{1+\lambda } \right)\] where (a, 0) and (0, a) are the coordinates of A and B respectively. Since, slope of \[AB=\frac{0-a}{a-0}=-1\]                 \[\therefore \]   Slope of \[MN=1\]         \[(\because \,MN\bot AB)\] Now, equation of MN \[y-\frac{\lambda a}{1+\lambda }=x-\frac{a}{1+\lambda }\]                 \[\Rightarrow \]               \[x-y=\frac{1-\lambda }{1+\lambda }a\] By putting \[x=0\]in this equation, we get the coordinates of M which are \[\left[ 0,\left( \frac{\lambda -1}{\lambda +1} \right)a \right].\] Now, it is given that area of\[\Delta AMN=\frac{3}{8}.\]area of \[\Delta OAB\] \[\Rightarrow \]               \[\frac{1}{2}\left| \begin{matrix}    1 & 1 & 1  \\    a & 0 & \frac{a}{1+\lambda }  \\    0 & \left( \frac{\lambda -1}{\lambda +1} \right) & \frac{\lambda a}{1+\lambda }  \\ \end{matrix} \right|=\frac{3}{8}.\frac{1}{2}{{a}^{2}}\] \[{{C}_{2}}\to {{C}_{2}}-{{C}_{1}}\]and \[{{C}_{3}}\to {{C}_{3}}-{{C}_{1}}\] \[\Rightarrow \]               \[\frac{1}{2}\left| \begin{matrix}    1 & 0 & 0  \\    a & -a & \frac{-a\lambda }{1+\lambda }  \\    0 & \left( \frac{\lambda -1}{\lambda +1} \right) & \frac{\lambda a}{1+\lambda }  \\ \end{matrix} \right|=\frac{3}{16}{{a}^{2}}\] \[\Rightarrow \]               \[\frac{1}{2}\left| -a\left( \frac{\lambda a}{1+\lambda } \right)+\frac{a\lambda }{1+\lambda }\left( \frac{\lambda -1}{\lambda +1} \right)a \right|=\frac{3}{16}{{a}^{2}}\]  \[\Rightarrow \] \[\frac{1}{2}\lambda {{a}^{2}}\left| \frac{\lambda -1}{{{(\lambda +1)}^{2}}}-\frac{1}{\lambda +1} \right|=\frac{3}{16}{{a}^{2}}\] \[\Rightarrow \]               \[\frac{1}{2}\lambda {{a}^{2}}\left| \frac{-2}{{{(\lambda +1)}^{2}}} \right|=\frac{3}{16}{{a}^{2}}\] \[\Rightarrow \]               \[\frac{\lambda {{a}^{2}}}{{{(\lambda +1)}^{2}}}=\frac{3}{16}{{a}^{2}}\] \[\Rightarrow \]               \[16\lambda =3{{\lambda }^{2}}+3+6\lambda \] \[\Rightarrow \]               \[3{{\lambda }^{2}}-10\lambda +3=0\] \[\Rightarrow \]               \[(\lambda -3)(3\lambda -1)=0\] \[\Rightarrow \]               \[\lambda =3\]or \[\lambda =\frac{1}{3}\] For \[\lambda =\frac{1}{3}.\,M\]lies outside the segment OB and hence the required value of \[\lambda \]is 3.                 ie,           \[\frac{AN}{BN}=3\]