question_answer

For \[x\in \left( 0,\frac{5\lambda }{2} \right)\], define \[f\left( x \right)=\int\limits_{0}^{x}{\sqrt{t}\sin t\,\,dt}\] Then \[f\] has.   AIEEE  Solved  Paper-2011

A) Local maximum at \[\pi \] and local \[2\pi \]

B) Local maximum at \[\pi \] and \[2\pi \]

C) Local minimum at \[\pi \] and \[2\pi \]

D) Local minimum at \[\pi \] and local maximum at \[2\pi \]

Correct Answer: A

Solution :

             We have, \[f\left( x \right)=\int\limits_{0}^{x}{\sqrt{t}}\sin t\,dt\] \[\Rightarrow \,\,\,f'\left( x \right)=\sqrt{x}\sin x\] For maximum or minimum value of \[f\left( x \right),f'\left( x \right)=0\] \[\Rightarrow \,\,x={{n}^{4\overline{\left){12}\right.}}}.\,n\square Z\] We observe that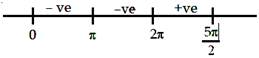              \[f'(x)\] changes its sign from \[+ve\] to \[-ve\] in the neighbourhood of \[\pi \] and \[-ve\] to \[+ve\] in the neighbourhood of \[2\pi \]. Hence \[f(x)\] has local maximum at \[x=\pi \] and local minima at \[x=2\pi \]