question_answer

Given\[P(x)={{x}^{4}}+a{{x}^{3}}+cx+d\]such that\[x=0\]is the only real root of\[P'(x)=0\]. If \[P(1)<P(1),\]then in the interval [-1, 1].     AIEEE  Solved  Paper-2009

A) P(-1) is the minimum and P(1) is the maximum of P

B) P(-1) is not minimum but P(1) is the maximum of P

C) P(-1) is the minimum but P(1) is not the maximum of P

D) neither P(-1) is the minimum nor P(1) is the maximum of P

Correct Answer: B

Solution :

\[P(x)={{x}^{4}}+a{{x}^{3}}+b{{x}^{2}}+cx+d\] \[P'(x)=4{{x}^{3}}+3a{{x}^{2}}+2bx+c\] As\[P'(x)=0\]has only root\[x=0\] \[\Rightarrow \] \[c=0\] \[P'(x)=x(4{{x}^{2}}+3ax+2b)\] \[\Rightarrow \]\[4{{x}^{3}}+3ax+2b=0\]has non real root. and\[4{{x}^{2}}+3ax+2b>0\forall x\in [-1,1]\].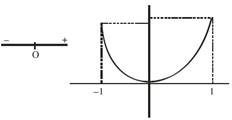 As P(−1) < P(1)\[\Rightarrow \]P(1) is the max. of\[P(x)\]in [−1, 1]