-
question_answer1) The ratio of the height of a tower and the length of its shadow on the ground is \[\sqrt{3}:1\]. What is the angle of elevation of the sun?
View Answer play_arrow
-
question_answer2) Volume and surface area of a solid hemisphere are numerically equal. What is the diameter of hemisphere?
View Answer play_arrow
-
question_answer3)
| A number is chosen at random from the numbers\[3,\text{ }2,\text{ }1,\text{ }0,\text{ }1,\text{ }2,\text{ }3\]. |
| What will be the probability that square of this number is less then or equal to 1? |
View Answer play_arrow
-
question_answer4) If the distance between the points \[(4,k)\] and \[(1,0)\] is 5, then what can be the possible values of k?
View Answer play_arrow
-
question_answer5) Find the roots of the quadratic equation \[\sqrt{2}{{x}^{2}}+7x+5\sqrt{2}=0\].
View Answer play_arrow
-
question_answer6) Find how many integers between 200 and 500 are divisible by 8?
View Answer play_arrow
-
question_answer7) Prove that tangents drawn at the ends of a diameter of a circle are parallel to each other.
View Answer play_arrow
-
question_answer8) Find the value of k for which the equation \[{{x}^{2}}+k(2x+k-1)+2=0\] has real and equal roots.
View Answer play_arrow
-
question_answer9) Draw a line segment of length 8 cm and divide it internally in the ratio \[4:5\].
View Answer play_arrow
-
question_answer10)
| In the given figure, PA and PB are tangents to the circle from an external point P. CD is another tangent touching the circle at Q. If\[PA=12\text{ }cm,\text{ }QC=QD=3\text{ }cm\], then find \[PC+PD\]. |
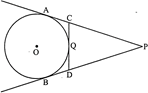 |
View Answer play_arrow
-
question_answer11) If \[{{m}^{th}}\] term of an A.P. is \[\frac{1}{n}\] and \[{{n}^{th}}\] term is \[\frac{1}{m}\], then find the sum of its first mn terms.
View Answer play_arrow
-
question_answer12) Find the sum of n terms of the series \[\left( 4-\frac{1}{n} \right)+\left( 4-\frac{2}{n} \right)+\left( 4-\frac{3}{n} \right)+.......\]
View Answer play_arrow
-
question_answer13) If the equation \[(1+{{m}^{2}}){{x}^{2}}+2mcx+{{c}^{2}}-{{a}^{2}}=0\] has equal roots then show that \[{{c}^{2}}={{a}^{2}}(1+{{m}^{2}})\].
View Answer play_arrow
-
question_answer14) The \[\frac{3}{4}th\] part of a conical vessel of internal radius 5 cm and height 24 cm is full of water. The water is emptied into a cylindrical vessel with internal radius 10 cm. Find the height of water in cylindrical vessel.
View Answer play_arrow
-
question_answer15)
| In the given figure, OACB is a quadrant of a circle with centre O and radius \[3.5\text{ }cm.\] If \[OD=2\text{ }cm\], find the area of the shaded region. |
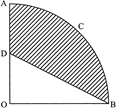 |
View Answer play_arrow
-
question_answer16) Two tangents TP and TQ are drawn to a circle with centre O from an external point T. Prove that \[\angle PTQ=2\angle OPQ.\]
View Answer play_arrow
-
question_answer17) Show that \[\Delta \,ABC\], where \[A(-2,0),B(2,0),C(0,2)\] and \[\Delta \text{ }PQR\] where \[P(-4,0),Q(4,0),R(0,4)\] are similar triangles.
View Answer play_arrow
-
question_answer18) The area of a triangle is 5 sq. units. Two of its vertices are (2, 1) and (\[3,\text{ }2\]). If the third vertex is \[\left( \frac{7}{2},y \right)\], find the value of y.
View Answer play_arrow
-
question_answer19)
| Two different dice are thrown together. Find the probability that the numbers obtained |
| (i) have a sum less than 7 |
| (ii) have a product less than 16 |
| (iii) is a doublet of odd numbers. |
View Answer play_arrow
-
question_answer20) A moving boat is observed from the top of a \[150\text{ }m\] high cliff moving away from the cliff. The angle of depression of the boat changes from \[60{}^\circ \] to \[45{}^\circ \] in 2 minutes. Find the speed of the boat in m/h.
View Answer play_arrow
-
question_answer21) Construct an isosceles triangle with base \[8\text{ }cm\] and altitude\[4\text{ }cm\]. Construct another triangle whose sides are \[\frac{2}{3}\] times the corresponding sides of the isosceles triangle.
View Answer play_arrow
-
question_answer22) Prove that the lengths of tangents drawn from an external point to a circle are equal.
View Answer play_arrow
-
question_answer23)
| The ratio of the sums of first m and first n terms of an A. P. is \[{{m}^{2}}:{{n}^{2}}\]. |
| Show that the ratio of its mth and nth terms is \[2(m-1):(2n-1)\]. |
View Answer play_arrow
-
question_answer24) Speed of a boat in still water is 15 km/h. It goes 30 km upstream and returns back at the same point in 4 hours 30 minutes. Find the speed of the stream.
View Answer play_arrow
-
question_answer25) If \[a\ne b\ne 0\], prove that the points \[(a,{{a}^{2}}),(b,{{b}^{2}})(0,0)\] will not be collinear.
View Answer play_arrow
-
question_answer26) The height of a cone is 10 cm. The cone is divided into two parts using a plane parallel to its base at the middle of its height Find the ratio of the volumes of the two parts.
View Answer play_arrow
-
question_answer27)
| Peter throws two different dice together and finds the product of the two numbers obtained. Rina throws a die and squares the number obtained. |
| Who has the better chance to get the number 25. |
View Answer play_arrow
-
question_answer28) A chord PQ of a circle of radius 10 cm subtends an angle of \[60{}^\circ \] at the centre of circle. Find the area of major and minor segments of the circle.
View Answer play_arrow
-
question_answer29) The angle of elevation of a cloud from a point 60 m above the surface of the water of a lake is \[30{}^\circ \] and the angle of depression of its shadow in water of lake is \[60{}^\circ \]. Find the height of the cloud from the surface of water.
View Answer play_arrow
-
question_answer30)
| In the given figure, the side of square is 28 cm and radius of each circle is half of the length of the side of the square where O and O? are centres of the circles. Find the area of shaded region. |
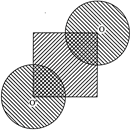 |
View Answer play_arrow
-
question_answer31) In a hospital used water is collected in a cylindrical tank of diameter 2 m and height 5 m. After recycling, this water is used to irrigate a park of hospital whose length is 25 m and breadth is 20 m. If tank is filled completely then what will be height of standing water used for irrigating the park. Write your views on recycling of water.
View Answer play_arrow



