-
question_answer1)
| In fig. 1, PQ is a tangent at a point C to a circle with centre O. If AB is a diameter and \[\angle CAB=30{}^\circ \], find \[\angle PCA\]. |
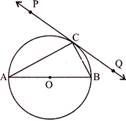 |
View Answer play_arrow
-
question_answer2) For what value of k will \[k+9,2k-1\] and \[2k+7\] are the consecutive terms of an A. P.?
View Answer play_arrow
-
question_answer3) A ladder, leaning against a wall/makes an angle of \[60{}^\circ \] with the horizontal. If the foot of the ladder is 2.5 m away from the wall, find the length of the ladder.
View Answer play_arrow
-
question_answer4) A card is drawn at random from a well shuffled pack of 52 playing cards. Find the probability of getting neither a red card nor a queen.
View Answer play_arrow
-
question_answer5) If \[5\] is a root of the quadratic equation \[2{{x}^{2}}+px-15=0\] and the quadratic equation \[p({{x}^{2}}+x)k=0\] has equal roots, find the value of k.
View Answer play_arrow
-
question_answer6) Let P and Q be the points of trisection of the line segment joining the points \[A(2,-2)\] and \[B(-7,4)\] such that P is nearer to A. Find the coordinates of P and Q.
View Answer play_arrow
-
question_answer7)
| In Fig. 2, a quadrilateral ABCD is drawn to circumscribe a circle, with centre O, in such a way that the sides AB, BC, CD and DA touch the circle at the points P, Q, R and S respectively. Prove that \[AB+CD=BC+DA\]. |
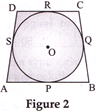 |
View Answer play_arrow
-
question_answer8) Prove that the points (3, 0), (6, 4) and (\[1,\text{ }3\]) are the vertices of a right angled isosceles triangle.
View Answer play_arrow
-
question_answer9) The 4th term of an A.P. is zero. Prove that the 25th term of the A.P. is three times its 11th term.
View Answer play_arrow
-
question_answer10)
| In Fig. 3, from an external point P, two tangents PT and PS are drawn to a circle with centre O and radius r. If \[OP=2r\], show that \[\angle OTS=\angle OST=30{}^\circ \]. |
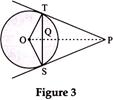 |
View Answer play_arrow
-
question_answer11)
| In fig. 4, O is the centre of a circle such that diameter \[AB=13\text{ }cm\] and \[AC=12\,cm.\,\,BC\] is joined Find the area of the shaded region. (Take\[\pi =3.14\]) |
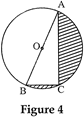 |
View Answer play_arrow
-
question_answer12)
| In fig. 5, a tent is in the shape of a cylinder surmounted by a conical top of same diameter. If the height and diameter of cylindrical part are 2.1 m and 3 m respectively and the slant height of conical part is 2.8 m, find the cost of canvas needed to make the tent if the canvas is available at the rate of Rs. 500/sq. metre. (Use \[\pi =\frac{22}{7}\] ) |
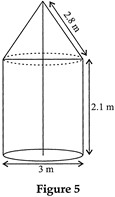 |
View Answer play_arrow
-
question_answer13) If the point \[P(x,y)\] is equidistant from the points \[A(a+b,b-a)\] and \[B(a-b,a+b)\]. Prove that \[bx=ay\].
View Answer play_arrow
-
question_answer14)
| In fig. 6, find the area of the shaded region, enclosed between two concentric circles of radii 7 cm and 14 cm where\[\angle AOC=40{}^\circ \]. (Use \[\pi =\frac{22}{7}\]) |
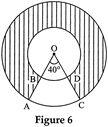 |
View Answer play_arrow
-
question_answer15) If the ratio of the sum of first n terms of two A.P?s is \[(7n+1):(4n+27)\], find the ratio of their \[{{m}^{th}}\] terms.
View Answer play_arrow
-
question_answer16) Solve for \[x:\frac{1}{(x-1)(x-2)}+\frac{1}{(x-2)(x-3)}=\frac{2}{3},x\ne 1,2,3\]
View Answer play_arrow
-
question_answer17) A conical vessel, with base radius 5 cm and height 24 cm, is full of water. This water is emptied into a cylindrical vessel of base radius 10 cm. Find the height to which the water will rise in the cylindrical vessel. (Use \[\pi =\frac{22}{7}\])
View Answer play_arrow
-
question_answer18) A sphere of diameter 12 cm, is dropped in a right circular cylindrical vessel, partly filled with water. If the sphere is completely submerged in water, the water level in the cylindrical vessel rises by \[\frac{32}{9}cm\]. Find the diameter of the cylindrical vessel.
View Answer play_arrow
-
question_answer19) A man standing on the deck of a ship, which is 10 m above water level, observes the angle of elevation of the top of a hill as \[60{}^\circ \] and the angle of depression of the base of hill as \[30{}^\circ \]. Find the distance of the hill from the ship and the height of the hill.
View Answer play_arrow
-
question_answer20) Three different coins are tossed together. Find the probability of getting (i) exactly two heads, (ii) at least two heads (iii) at least two tails.
View Answer play_arrow
-
question_answer21) Due to heavy floods in a state, thousands were rendered homeless. 50 schools collectively offered to the state government to provide place and the canvas for 1500 tents to be fixed by the government and decided to share the whole expenditure equally. The lower part of each tent is cylindrical of base radius 2.8 m and height 3.5 m, with conical upper part of same base radius but of height 2.1 m. If the canvas used to make the tents costs Rs. 120 per sq. m, find the amount shared by each school to set up the tents. What value is generated by the above problem? (Use \[\pi =\frac{22}{7}\])
View Answer play_arrow
-
question_answer22) Prove that the lengths of the tangents drawn from an external point to a circle are equal.
View Answer play_arrow
-
question_answer23) Draw a circle of radius 4 cm. Draw two tangents to the circle inclined at an angle of \[60{}^\circ \] to each other.
View Answer play_arrow
-
question_answer24)
| In Fig. 7, two equal circles, with centres O and O?, touch each other at X. OO? produced meets the circle with centre O? at A. AC is tangent to the circle with centre O, at the point C. O'D is perpendicular AC. Find the value of \[\frac{DO'}{CO}\] . |
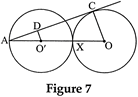 |
View Answer play_arrow
-
question_answer25) Solve for \[x:\frac{1}{x+1}+\frac{2}{x+2}=\frac{4}{x+4},x\ne -1,-2,-4\]
View Answer play_arrow
-
question_answer26) The angle of elevation of the top Q of a vertical tower PQ from a point X on the ground is \[60{}^\circ \]. From a point Y, 40 m vertically above X, the angle of elevation of the top Q of tower is \[45{}^\circ \]. Find the height of the tower PQ and the distance PX (Use \[\sqrt{3}=1.73\])
View Answer play_arrow
-
question_answer27) The houses in a row are numbered consecutively from 1 to 49. Show that there exists a value of X such that sum of numbers of houses proceeding the house numbered X is equal to sum of the numbers of houses following X.
View Answer play_arrow
-
question_answer28)
| In fig. 8, the vertices of \[\Delta \,ABC\] are \[A(4,6),\,\,B(1,5)\]and \[C(7,2)\]. A line ? segment DE is drawn to intersect the sides AB and AC at D and E respectively such that \[\frac{AD}{AB}=\frac{AE}{AC}=\frac{1}{3}\]. Calculate the area of \[\Delta \,ADE\] and compare it with area of \[\Delta \,ABC\]. |
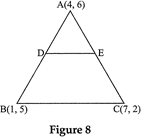 |
View Answer play_arrow
-
question_answer29) A number x is selected at random from the numbers 1, 2, 3 and 4. Another number y is selected at random from the numbers 1, 4, 9 and 16. Find the probability that product of x and y is less than 16.
View Answer play_arrow
-
question_answer30)
| In Fig. 9, is shown a sector OAP of a circle with centre O, containing \[\angle \theta .\text{ }AB\] is perpendicular to the radius OA and meets OP produced at B. Prove that the perimeter of shaded region is \[r\left[ \tan \,\theta +\sec \,\theta +\frac{\pi \theta }{180}-1 \right]\] |
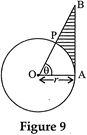 |
View Answer play_arrow
-
question_answer31) A motor boat whose speed is 24 km/h in still water takes 1 hour more to go 32 km upstream than to return downstream to the same spot. Find the speed of the stream.
View Answer play_arrow









