question_answer

P and Q are two points observed from the top of a building \[10\sqrt{3}\] m high. If the angles of depression of the points are complementary and PQ = 20 m, then the distance off from the building is

A)  25 m   

B)  45 m

C)  30 m               

D)  40 m

Correct Answer: C

Solution :

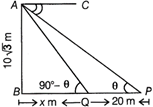\[AB=\,\,Builiding=10\sqrt{3}\,\,m\] \[PQ=20\,\,m\] \[BQ=x\,\,m\]             If \[\angle APB=\theta ,\] then \[\angle AQB=90{}^\circ -\theta \] From \[\Delta \,\,ABP,\tan \theta =\frac{AB}{BP}=\frac{10\sqrt{3}}{x+20}\]        ?(i) From \[\Delta \,\,ABQ,\,\,\tan (90{}^\circ -\theta )=\frac{AB}{BQ}\]                      \[\Rightarrow \]   \[\cot \theta =\frac{10\sqrt{3}}{x}\]                    ?(ii) By multiplying both equations, \[\tan \theta \cdot \cot \theta =\frac{10\sqrt{3}}{x+20}\times \frac{10\sqrt{3}}{x}\] \[\Rightarrow \]   \[{{x}^{2}}+20x=10\times 10\times 3\] \[\Rightarrow \]   \[{{x}^{2}}+20x-300=0\] \[\Rightarrow \]   \[{{x}^{2}}+30x-10x-300=0\] \[\Rightarrow \]   \[x(x+30)-10(x+30)=0\] \[\Rightarrow \]   \[(x-10)(x+30)=0\] \[\Rightarrow \]     \[x=10,\ne -30\]