question_answer

In \[\Delta ABC,\,AB=BC=K,AC=\sqrt{2}K,\]then \[\Delta ABC\]is a:

A)  Isosceles triangle     

B)  Right angled triangle

C)  Equilateral triangle    

D)  Right isosceles triangle

Correct Answer: D

Solution :

In  \[\Delta ABC\]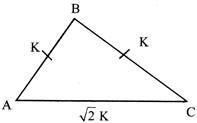 \[AC=\sqrt{2}K\] \[A{{C}^{2}}=2{{K}^{2}}\] \[A{{C}^{2}}=A{{B}^{2}}+B{{C}^{2}}\] So \[\Delta \text{ }ABC\]is right angled triangle So, in \[\Delta \text{ }ABC\] \[\frac{AB}{AC}=\frac{K}{\sqrt{2}K}=\frac{1}{\sqrt{2}}\] So  \[\cos \theta =\frac{1}{\sqrt{2}}\] \[\theta ={{45}^{o}}\] So, \[ABC,\text{ }\angle B={{90}^{o}};\text{ }\angle C={{45}^{o}};\text{ }\angle A={{45}^{o}}\]So, ABC is right is oscles triangle.