question_answer

The relatives velocity of a car A with respect to car B is \[30\sqrt{2}\,m/s\] due north-east. The velocity of car B is \[20m/s\] due south. The relative velocity of car C with respect to car A is \[10\sqrt{2}m/s\] due north weast. The speed of car c and the direction (in terms of angle it makes with the east) are respectively:

A)  \[20\sqrt{2}m/s,\,{{45}^{o}}\]     

B)  \[20\sqrt{2}m/s,\,{{135}^{o}}\]

C)  \[10\sqrt{2}\,m/s,\,{{45}^{o}}\]

D)  \[10\sqrt{2}\,m/s,\,{{135}^{o}}\]

Correct Answer: A

Solution :

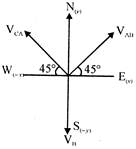From the diagram (above), we get             \[{{V}_{CA}}={{V}_{A}}-{{V}_{B}}\]                 \[=30\sqrt{2}\,(\cos {{45}^{o}}i+\sin {{45}^{o}})\]                 \[=(30i+30j)m/s\]                 \[{{V}_{B}}=(-20j)m/s\] (given)                 \[{{V}_{CA}}={{V}_{C}}-{{V}_{A}}\]                 \[=10\sqrt{2}\,(-\cos \,{{45}^{o}}i+\sin {{45}^{o}}j)\]                 \[=(-10i+10j)m/s\]                 \[{{V}_{C}}=20i+20j\]                 \[|{{V}_{C}}|\,\,=\sqrt{{{20}^{2}}+{{20}^{2}}}=20\sqrt{2}\] and       \[\tan \theta =20/20\]  \[\Rightarrow \]  \[\theta ={{45}^{o}}\]