A) \[20\sqrt{2}m/s,\,{{45}^{o}}\]
B) \[20\sqrt{2}m/s,\,{{135}^{o}}\]
C) \[10\sqrt{2}\,m/s,\,{{45}^{o}}\]
D) \[10\sqrt{2}\,m/s,\,{{135}^{o}}\]
Correct Answer: A
Solution :
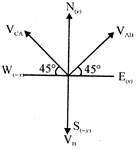 From the diagram (above), we get \[{{V}_{CA}}={{V}_{A}}-{{V}_{B}}\] \[=30\sqrt{2}\,(\cos {{45}^{o}}i+\sin {{45}^{o}})\] \[=(30i+30j)m/s\] \[{{V}_{B}}=(-20j)m/s\] (given) \[{{V}_{CA}}={{V}_{C}}-{{V}_{A}}\] \[=10\sqrt{2}\,(-\cos \,{{45}^{o}}i+\sin {{45}^{o}}j)\] \[=(-10i+10j)m/s\] \[{{V}_{C}}=20i+20j\] \[|{{V}_{C}}|\,\,=\sqrt{{{20}^{2}}+{{20}^{2}}}=20\sqrt{2}\] and \[\tan \theta =20/20\] \[\Rightarrow \] \[\theta ={{45}^{o}}\]
From the diagram (above), we get \[{{V}_{CA}}={{V}_{A}}-{{V}_{B}}\] \[=30\sqrt{2}\,(\cos {{45}^{o}}i+\sin {{45}^{o}})\] \[=(30i+30j)m/s\] \[{{V}_{B}}=(-20j)m/s\] (given) \[{{V}_{CA}}={{V}_{C}}-{{V}_{A}}\] \[=10\sqrt{2}\,(-\cos \,{{45}^{o}}i+\sin {{45}^{o}}j)\] \[=(-10i+10j)m/s\] \[{{V}_{C}}=20i+20j\] \[|{{V}_{C}}|\,\,=\sqrt{{{20}^{2}}+{{20}^{2}}}=20\sqrt{2}\] and \[\tan \theta =20/20\] \[\Rightarrow \] \[\theta ={{45}^{o}}\]
You need to login to perform this action.
You will be redirected in
3 sec
