question_answer

A particle of mass 4m which is at rest explodes into three fragments. Two of the fragments each of mass m are found to move with a speed V each is mutually perpendicular direction. The energy released in the process of explosion will be:

A)  \[1/4m{{V}^{2}}\]             

B)  \[3/2m{{V}^{2}}\]

C)  \[1/2m{{V}^{2}}\]             

D)  \[3/4m{{V}^{2}}\]

Correct Answer: B

Solution :

From the law of conservation of momentum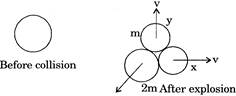 From question, initial momentum = 0, so that final momentum should be zero. Let V be the velocity of mass 2m then \[\therefore \]    \[\sqrt{{{(mV)}^{2}}+{{(mV)}^{2}}}=2m{{V}_{1}}\] or         \[{{V}_{1}}=\frac{V}{\sqrt{2}}\]                           .....(i) \[\therefore \] K.E. Total = K.E (First piece) + K.E. (Second piece) + K.E (Third piece)             \[K\,E=\frac{1}{2}m{{V}^{2}}+\frac{1}{2}(2m){{V}_{1}}^{2}\]             \[=2\left( \frac{1}{2}m{{V}^{2}} \right)+m\left( \frac{{{V}^{2}}}{2} \right)\] \[\Rightarrow \]            \[K.{{E}_{after\,\,\exp losion}}=\frac{3}{2}m{{V}^{2}}\] Also, \[K.{{E}_{Before\,\,\exp losion}}=0\] Hence, Piece in K.E \[=\frac{3}{2}m{{V}^{2}}\]