A) \[\sqrt{2}\,m/s\]
B) \[2\sqrt{2}\,m/s\]
C) \[2\,m/s\]
D) \[4\sqrt{2}\,m/s\]
Correct Answer: B
Solution :
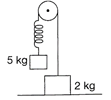
Hence, the correction option is (a). Let \[x\]be the extension in the spring when 2 kg block leaves contact with the ground. \[\therefore \]\[Kx=2g\]or \[x=\frac{2g}{K}=\frac{2\times 10}{40}=\frac{1}{2}m\] From conservation of mechanical energy (for m = 5 kg block), \[mgx=\frac{1}{2}K{{x}^{2}}+\frac{1}{2}m{{v}^{2}}\] \[5\times 10\times \frac{1}{2}=\frac{1}{2}\times 40\times {{\left( \frac{1}{2} \right)}^{2}}+\frac{1}{2}\times 5{{v}^{2}}\] \[25=5+\frac{5}{2}{{v}^{2}}\] \[v=\sqrt{8}=2\sqrt{2}\,m/s\] Hence, the correction option is (b).You need to login to perform this action.
You will be redirected in
3 sec
