A) \[\frac{M{{\omega }_{0}}}{M+3m}\]
B) \[\frac{M{{\omega }_{0}}}{M+6m}\]
C) \[\frac{M+6m}{M}{{\omega }_{0}}\]
D) \[{{\omega }_{0}}\]
Correct Answer: B
Solution :
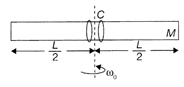
Suppose, when the leads reach the ends, moment of inertia of the system changes from \[{{\text{I}}_{\text{1}}}\]to \[{{\text{I}}_{2}}\]an therefore, The angular velocity changes from \[{{\omega }_{1}}\]to\[{{\omega }_{2}}.\] as External torque acting on the system is zero, hence Angular momentum of the system is conserved. i.e., \[{{I}_{1}}{{\omega }_{1}}={{I}_{2}}{{\omega }_{2}}\] \[[{{\omega }_{0}}={{\omega }_{1}}\,\text{here}]\] \[\left\{ \frac{M{{L}^{2}}}{12}+0 \right\}{{\omega }_{0}}=\left\{ \frac{M{{L}^{2}}}{12}+2m{{\left( \frac{L}{2} \right)}^{2}} \right\}{{\omega }_{2}}\] \[\therefore \]\[{{\omega }_{2}}=\left\{ \frac{M{{L}^{2}}/12}{\frac{M{{L}^{2}}}{12}+\frac{m{{L}^{2}}}{2}} \right\}{{\omega }_{0}}\]or \[{{\omega }_{2}}=\left\{ \frac{M}{M+6m} \right\}{{\omega }_{0}}\] Hence, the correction option is (b).You need to login to perform this action.
You will be redirected in
3 sec
