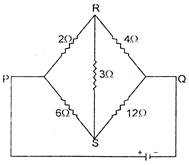
A) \[8\,\Omega \]
B) \[1.5\,\Omega \]
C) \[4.5\,\Omega \]
D) \[6\,\Omega \]
Correct Answer: C
Solution :
The arms PR, RQ, QS and SP satisfy the condition required to form a balanced Wheatstone bridge. Therefore point RS are at the same potential and resistance, so no current flows through middle resistance RS of 3Q will not be taken into consideration. As it is clear that the resistances of the upper arm are connected in series. Hence, their equivalent resistence is \[{{R}_{U}}=2+4=6\Omega \] Similarly, resistance of lower arm which are also connected in series. Hence their equivalent resistance is \[{{R}_{L}}=6+12=18\,\Omega \] Since resistance \[{{R}_{U}}\] and \[{{R}_{L}}\]is connected in parallel combination. Therefore, the equivalent resistance between points P and Q is: \[\frac{1}{{{R}_{PQ}}}=\frac{1}{6}+\frac{1}{18}=\frac{4}{18}\]You need to login to perform this action.
You will be redirected in
3 sec
