A) \[\frac{F}{2}\]towards right
B) \[\frac{F}{3}\]towards left
C) \[\frac{2F}{3}\] towards right
D) 0
Correct Answer: D
Solution :
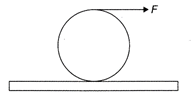
Let f be the force of friction on the ring which is directed to the right, a be the acceleration of its center of mass and\[\alpha \]the angular acceleration as shown in the figure. The point of contact P is at instantaneous rest so the ring rotates about P.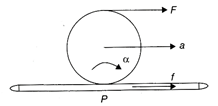 \[\therefore \]\[\alpha =\frac{{{\tau }_{P}}}{{{I}_{P}}}=\frac{F(2R)}{2M{{R}^{2}}}=\frac{F}{MR}\] As \[F+f=Ma=M(R\alpha )=F\]\[\therefore \]\[f=0\]
\[\therefore \]\[\alpha =\frac{{{\tau }_{P}}}{{{I}_{P}}}=\frac{F(2R)}{2M{{R}^{2}}}=\frac{F}{MR}\] As \[F+f=Ma=M(R\alpha )=F\]\[\therefore \]\[f=0\]
You need to login to perform this action.
You will be redirected in
3 sec
