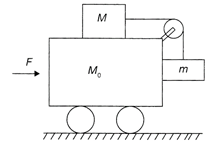
A) If F = 0 blocks cannot remain stationary
B) For one unique value of F, blocks will be stationary
C) Blocks cannot be stationary for any value of F because all surfaces are smooth
D) Both (1) and (2)
Correct Answer: D
Solution :
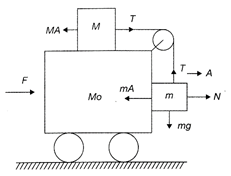 Let us assume that the blocks do not move with respect to the trolley if the acceleration of the trolley is A. Making observations with respect to ground: \[F=(M+m+{{m}_{o}})A\Rightarrow A=\frac{F}{(M+m+{{m}_{o}})}\] Making observations with respect to the trolley: \[T=MA,T=mg\] \[\Rightarrow \]\[MA=mg\Rightarrow \frac{MF}{(M+m+{{m}_{o}})}=mg\] \[\therefore \] \[F=\frac{(M+m+{{m}_{o}})mg}{M}\] Thus for \[F=\frac{(M+m+{{m}_{o}})mg}{M}\]the blocks remain at rest with respect to the trolley. From above relations for F = 0, A = 0 and T = 0, so the blocks move with respect to the trolley if F=0. Hence, the correction option is (d).
Let us assume that the blocks do not move with respect to the trolley if the acceleration of the trolley is A. Making observations with respect to ground: \[F=(M+m+{{m}_{o}})A\Rightarrow A=\frac{F}{(M+m+{{m}_{o}})}\] Making observations with respect to the trolley: \[T=MA,T=mg\] \[\Rightarrow \]\[MA=mg\Rightarrow \frac{MF}{(M+m+{{m}_{o}})}=mg\] \[\therefore \] \[F=\frac{(M+m+{{m}_{o}})mg}{M}\] Thus for \[F=\frac{(M+m+{{m}_{o}})mg}{M}\]the blocks remain at rest with respect to the trolley. From above relations for F = 0, A = 0 and T = 0, so the blocks move with respect to the trolley if F=0. Hence, the correction option is (d).
You need to login to perform this action.
You will be redirected in
3 sec
