| Find \[{{A}^{-1}},\] if \[A=\left[ \begin{matrix} 0 & 1 & 1 \\ 1 & 0 & 1 \\ 1 & 1 & 0 \\ \end{matrix} \right]\] and show that \[{{A}^{-1}}=\frac{{{A}^{2}}-3I}{2}.\] |
| OR |
| If \[A=\left[ \begin{matrix} 1 & -\,1 & 1 \\ 2 & 1 & -\,3 \\ 1 & 1 & 1 \\ \end{matrix} \right],\] find \[{{A}^{-1}}\] and hence solve the system of linear equation \[x+2y+z=4,\] \[-\,x+y+z=0,\] \[x-3y+z=2.\] |
Answer:
We have, 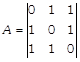
Clearly, 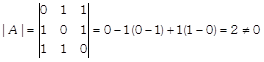
\[\therefore \] \[{{A}^{-1}}\] exists. Now, let us evaluate the cofactors of elements of \[|A|.\] Clearly, \[{{C}_{11}}={{(-\,1)}^{1+1}}\left| \begin{matrix} 0 & 1 \\ 1 & 0 \\ \end{matrix} \right|=-\,1\] \[{{C}_{21}}={{(-\,1)}^{2+1}}\left| \begin{matrix} 1 & 1 \\ 1 & 0 \\ \end{matrix} \right|=1,\] \[{{C}_{31}}={{(-\,1)}^{3+1}}\left| \begin{matrix} 1 & 1 \\ 0 & 1 \\ \end{matrix} \right|=1,\] \[{{C}_{12}}={{(-\,1)}^{1+2}}\left| \begin{matrix} 1 & 1 \\ 1 & 0 \\ \end{matrix} \right|=1,\] \[{{C}_{22}}={{(-\,1)}^{2+2}}\left| \begin{matrix} 0 & 1 \\ 1 & 0 \\ \end{matrix} \right|=1,\] \[{{C}_{32}}={{(-\,1)}^{3+2}}\left| \begin{matrix} 0 & 1 \\ 1 & 1 \\ \end{matrix} \right|=1,\] \[{{C}_{13}}={{(-\,1)}^{1+3}}\left| \begin{matrix} 1 & 0 \\ 1 & 1 \\ \end{matrix} \right|=1,\] \[{{C}_{23}}={{(-\,1)}^{2+3}}\left| \begin{matrix} 0 & 1 \\ 1 & 1 \\ \end{matrix} \right|=1\] and \[{{C}_{33}}={{(-\,1)}^{3+3}}\left| \begin{matrix} 0 & 1 \\ 1 & 0 \\ \end{matrix} \right|=-1\] \[\therefore \]adj 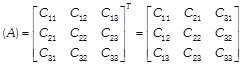
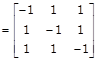
Thus, \[{{A}^{-1}}=\frac{1}{|A|}\] adj 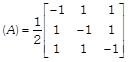
Now, consider 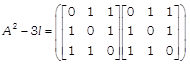
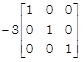
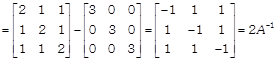
Hence proved. OR We have, 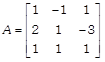
Clearly, 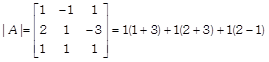
\[=4+5+1=10\ne 0\] \[\therefore \] \[{{A}^{-1}}\] exist. Now, let us find the cofactors \[{{C}_{ij}}\] of elements \[{{a}_{ij}}\]in A. Clearly, \[{{C}_{11}}={{(-\,1)}^{1+1}}\left| \begin{matrix} 1 & -\,3 \\ 1 & 1 \\ \end{matrix} \right|=4,\] \[{{C}_{12}}={{(-1)}^{2+1}}\left| \begin{matrix} 2 & -\,3 \\ 1 & 1 \\ \end{matrix} \right|=-\,5,\] \[{{C}_{13}}={{(-1)}^{1+3}}\left| \begin{matrix} 2 & 1 \\ 1 & 1 \\ \end{matrix} \right|=1,\] \[{{C}_{21}}={{(-\,1)}^{2+1}}\left| \begin{matrix} -\,1 & 1 \\ 1 & 1 \\ \end{matrix} \right|=2,\] \[{{C}_{22}}={{(-\,1)}^{2+2}}\left| \begin{matrix} 1 & 1 \\ 1 & 1 \\ \end{matrix} \right|=0,\] \[{{C}_{23}}={{(-\,1)}^{2+3}}\left| \begin{matrix} 1 & -\,1 \\ 1 & 1 \\ \end{matrix} \right|=-\,2,\] \[{{C}_{31}}={{(-\,1)}^{3+1}}\left| \begin{matrix} -\,1 & 1 \\ 1 & -\,3 \\ \end{matrix} \right|=2,\] \[{{C}_{32}}={{(-\,1)}^{3+2}}\left| \begin{matrix} 1 & 1 \\ 2 & -\,3 \\ \end{matrix} \right|=5,\] \[{{C}_{33}}={{(-\,1)}^{3+3}}\left| \begin{matrix} 1 & -\,1 \\ 2 & 1 \\ \end{matrix} \right|=3\] \[\therefore \] adj 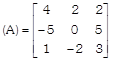
\[\Rightarrow \] 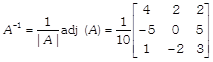 ?(i)
?(i) Now, let us solve the given system of linear equations which can be written in matrix form as 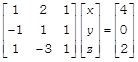
OR \[{{A}^{T}}X=B,\] where 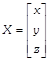 and
and ![]()
Since, \[|{{A}^{T}}|\,\,=\,\,|A|\,\,=10\ne 0.\] So, the given system of equations is consistent and have a unique solution given by \[X={{({{A}^{T}})}^{-1}}B={{({{A}^{-1}})}^{T}}B\] 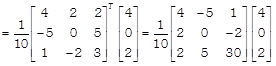
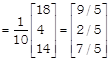
\[\Rightarrow \] \[x=\frac{9}{5},\] \[y=\frac{2}{5}\] and \[z=\frac{7}{5},\] which is the required solution.
You need to login to perform this action.
You will be redirected in
3 sec
