| In the given fig. what is the ratio of the areas of |
| (a) shaded portion I to shaded portion II? |
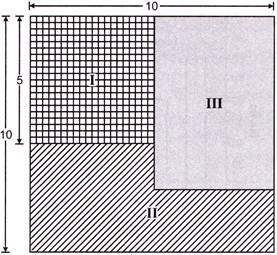 |
| (b) shaded portion II to shaded portion III? |
| (c) shaded portions I and II taken together and shaded portion III? |
Answer:
By splitting the above figure, we get, 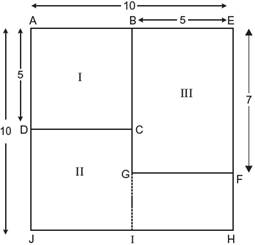
(a) Now, \[~AD=5\] \[AB=AEBE=105\] \[AB=5\] Area of shaded portion I = Area of ABCD \[\therefore \] Area of \[ABCD=AD\times AB=5\times 5=25\] So, Area of shaded portion \[I=25\] Area of shaded portion II = Area of DCIJ ? Area FHI Now, \[DJ=AJAD=105=5\] \[DC=AB\](as It?s a square) \[DC=5\] of \[DCIJ=DJ\times DC=5\times 5=25\] Now, \[AJ=EH\] (side of a square) \[EH=10\] So, \[FH=EHEF=107\] \[FH=3\] and \[GF=BE\] \[GF=5\] area \[GFHI=GF\times FH\] \[=5\times 3=15\] Area o shaded portion \[II=25+15=40\] So, required ratio of shaded portion I to II is \[25:40\] \[=\frac{25}{40}=\frac{5\times 5}{8\times 5}\] \[=\frac{5}{8}=5:8\] (b) Area of shaded portion III = Area of BEFG \[=BE\times EF\] \[=5\times 7\] \[=35\] So, required ratio of shaded portion II to III is \[40:35\] \[=\frac{40}{35}=\frac{8\times 5}{7\times 5}=\frac{8}{7}\] \[=8:7\] (c) Area of shaded portions I and II = 25 + 40 = 65 So, required ratio \[=65:35\] \[=\frac{65}{35}=\frac{13\times 5}{7\times 5}=\frac{13}{7}\] \[=13:7\]
You need to login to perform this action.
You will be redirected in
3 sec
