question_answer

Draw a circle with centre C and radius 3.4 cm. Draw any chord\[\overline{AB}\]. Construct the perpendicular bisector of \[\overline{AB}\] and examine if it passes through C.

Answer:

To construct the perpendicular bisector of chord \[\overline{AB}\]. we use the following steps:

Step I: Draw a circle with C as centre and radius 3.4 cm.

Step II: Now, draw a chord AB of the circle (a chord of a circle is a line segment joining any two points on the circle)

Step III: With A as centre, using compasses draw an arc (here, we can draw circle also) with radius more than half of the length of \[\overline{AB}\].

Step IV: With the same radius and with B as centre, draw an another arc using compasses.

Let it cut the previous arc at P and C.

Step V: Join \[\overline{PC}\] and produce up to Q. It cuts \[\overline{AB}\] at O. Therefore, \[\overline{PC}\] is the perpendicular bisector of \[\overline{AB}\].

Also, the perpendicular bisector \[\overline{PB}\] passes through the centre C of the circle.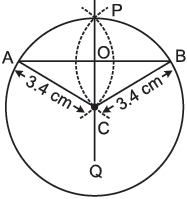

Hence, the perpendicular bisector of chord AB passes through the centre C.