question_answer

A fruit grower can use two types of fertilisers in his garden, brand P and brand Q. The amounts (in kg) of nitrogen, phosphoric acid, potash and chlorine in a bag of each brand are given in the table. Tests indicate that the garden needs at least 240 kg of phosphoric acid, at least 270 kg of potash and almost 310 kg of chlorine. If the grower wants to maximise the amount of nitrogen added to the garden, how many bags of each brand should be added? What is the maximum amount of nitrogen added?

	Brand P	Brand Q
Nitrogen	3	3.5
Phosphoric acid	1	2
Potash	3	1.5
Chlorine	1.5	2

Answer:

Let the fruit grower mixes x bags of brand P and y bags brand 0. Then, given information can be written in table form as

Brand of fertiliser	Numnber of bags	Amount of nitrogen	Amount of phosphoric acid	Amount of potash	Amount of chlorine
P	x	3x	1 x	3x	1.5 x
A	y	3.5y	2 y	1.5 y	2y
Total	\[x+y\]	\[3x+3.5y\]	\[x+2y\]	\[3x+1.5y\]	\[1.5x+2y\]

Our problem is to maximise \[Z=3x+3.5\text{ }y\] Subject to the constraints \[x+2y\ge 240\] \[3x+1.5y\ge 270\]             \[1.5x+2y\le 310\] and       \[x\ge 0,\] \[y\ge 0\]                 Consider the above inequality as equation, we get \[x+2y=240\]                            ...(i) \[3x+1.5y=270\]                                    ...(ii) \[1.5x+2y=310\]                                    ...(iii) and       x = 0, y = 0                              ...(iv) Table for the line \[x+2y=240\] is

x	0	240
y	120	0

So, line \[x+2y=240\] passes through the points (0, 120) and (240, 0). On putting (0, 0) in the inequality \[x+2y\ge 240,\]we get             \[0+2\times 0\ge 240\] \[\Rightarrow \] \[0\ge 240\]  [false] So, the half plane is away from the origin. Table for the line \[3x+1.5y=270\]

x	0	90
y	180	0

So, line \[3x+1.5y=270\] passes through the points (0, 180) and (90, 0).                          On putting (0, 0) in the inequality \[3x+1.5y\ge 270,\]  we get \[3\times 0+1.5\times 0\ge 270\] \[\Rightarrow \] \[0\ge 270\] [false] So, the half plane is away from the origin. Table for the line \[1.5x+2y=310\] is

x	0	620/3
y	155	0

So, line \[1.5x+2y=310\] passes through the points (0, 155) and \[\left( \frac{620}{3},\,\,0 \right).\] On putting (0, 0) in the inequality \[1.5x+2y\le 310,\] We get \[1.5\times 0+2\times 0\le 310\] \[\Rightarrow \] \[0\le 310\]   [true] So, the half plane is towards the origin. The intersection point of lines (ii) and (iii) is 8(20, 140), of lines (iii) and (i) is A(140, 50), of lines (i) and (ii) is C(40, 100). Since, \[x,\,\,y\ge 0\] So, the feasible region lies in the first quadrant.   On plotting the graph, we get the feasible region CABC, whose corner points are 0(40, 100), A (140, 50)and B(20, 140). Now, the values of Z at these points are as follows

Corner points	\[\mathbf{Z=3x+3}\mathbf{.5y}\]
A(140, 50)	\[Z=3\times 140+3.5\times 50\] = 595 (maximum)
B(20, 140)	\[Z=3\times 20+3.5\times 140=550\]
C(40, 100)	\[Z=3\times 40+3.5\times 100=470\]

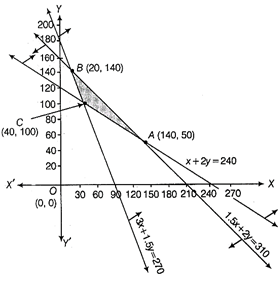The maximum value of Z is 595 and It is occur at A(140, 50). Hence, 140 bags of brand P and 50 bags of brand Q should be added to the garden to maximise the amount of nitrogen and maximum amount of nitrogen added to the garden is 595 kg.