Answer:
So to find the line or symmetry of angle \[75{}^\circ \], we use the following steps: Step I: Draw \[\overline{AB}\]of any length. Step II: Place the centre of the protractor at A and the zero edge along \[\overline{AB}\]. 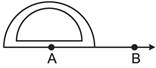
Step III: Start with zero near B, mark point C at \[75{}^\circ \]. 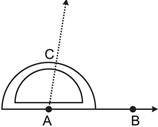
Step IV: Join AC. \[\angle BAC\]is the required angle of measure \[75{}^\circ \]. 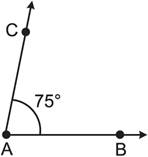
Step V: With A as centre and using compasses, draw an arc that cuts both rays of \[\angle A\] at P and \[Q\]. 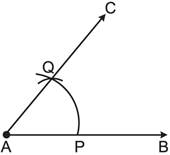
Step VI: With P as centre, draw (in the interior of \[\angle A\] an arc whose radius is more than half of the length of\[PQ\]). Step VII: With the same radius and with Q as centre, draw another arc in the interior of \[\angle A\]. Let the two arcs intersect at D. 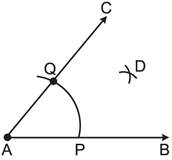
Step VIII: Join AD, then is \[\overline{AD}\]the required bisector of \[\angle A\], i.e., AD is the line of symmetry of an angle of measure \[75{}^\circ \]. 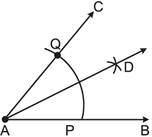
You need to login to perform this action.
You will be redirected in
3 sec
