question_answer

Find the shortest distance between lines \[\frac{x-3}{1}=\frac{y-5}{-\,2}=\frac{z-7}{1}\] and       \[\frac{x+1}{7}=\frac{y+1}{-\,6}=\frac{z+1}{1}.\]

Answer:

Given equations of lines are                         \[\frac{x-3}{1}=\frac{y-5}{-\,2}=\frac{z-7}{1}\]              ?(i)             and       \[\frac{x+1}{7}=\frac{y+1}{-\,6}=\frac{z+1}{1}\]                    ?(ii) On comparing above equations with one point form of equation of line which is             \[\frac{x-{{x}_{1}}}{a}=\frac{y-{{y}_{1}}}{b}=\frac{z-{{z}_{1}}}{c},\] we get \[{{a}_{1}}=1,\] \[{{b}_{1}}=-\,2,\] \[{{c}_{1}}=1,\] \[{{x}_{1}}=3,\]             \[{{y}_{1}}=5,\] \[{{z}_{1}}=7\] and       \[{{a}_{2}}=7,\] \[{{b}_{2}}=-\,6,\]             \[{{c}_{2}}=1,\] \[{{x}_{2}}=-\,1,\]             \[{{y}_{2}}=-\,1,\] \[{{z}_{2}}=-\,1\] We know that the shortest distance between two lines is given by 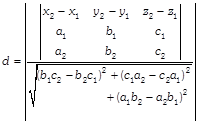\[\therefore \]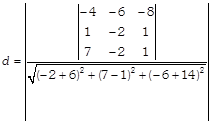 \[=\left| \frac{-\,4(-2\,+6)+6(1-7)-8(-\,6+14)}{\sqrt{{{(4)}^{2}}+{{(6)}^{2}}+{{(8)}^{2}}}} \right|\] \[=\left| \frac{-\,4(4)+6(-6)-8(8)}{\sqrt{16+36+64}} \right|\] \[=\left| \frac{-\,16-36-64}{\sqrt{116}} \right|\] \[=\left| \frac{-\,116}{\sqrt{116}} \right|=\frac{116}{\sqrt{116}}\] \[=\frac{{{(\sqrt{116})}^{2}}}{\sqrt{116}}=\sqrt{116}\] Hence, the required shortest distance is \[\sqrt{116}\]units.