question_answer

The centre of the circle passing through the point \[\left( \mathbf{0},\mathbf{1} \right)\] and touching the curve \[\mathbf{y}={{\mathbf{x}}^{\mathbf{2}}}\] at \[\left( \mathbf{2},\mathbf{4} \right)\]is:

A) \[\left( \frac{-16}{5},\frac{27}{10} \right)\]          

B) \[\left( \frac{-16}{7},\frac{53}{10} \right)\]  

C) \[\left( \frac{-16}{5},\frac{53}{10} \right)\]          

D) \[\left( \frac{16}{5},\frac{-53}{10} \right)\]

Correct Answer: C

Solution :

[c] Let the centre of circle be \[\left( \alpha ,\beta  \right)\]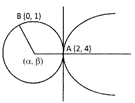 \[\therefore O{{A}^{2}}=O{{B}^{2}}\] \[{{\alpha }^{2}}+{{(\beta -1)}^{2}}={{(\beta -2)}^{2}}+{{(\beta -4)}^{2}}\] \[{{\alpha }^{2}}+{{\beta }^{2}}-2\beta +1\] \[={{\alpha }^{2}}-4\alpha +4+{{\beta }^{2}}-8\beta +16\] \[=4\alpha +6\beta -19=0\]                       .......(1) Slope of \[OA=\frac{\beta -4}{\alpha -2}\] Slope of tangent at \[\left( 2,4 \right)\] to \[y={{x}^{2}}\]be \[{{y}_{1}}at(2,4)=2x=2\times 2=4\] Since, (slope of OA) (slope of tangent at \[(A)=-1\] \[\frac{\beta -1}{\alpha -2}\times 4=-1\] \[\Rightarrow 4\beta -16=-\alpha +2\] \[\Rightarrow \alpha +4\beta -18\]                        ??...,.(2) Solving equation (1) and (2), we have \[\frac{\alpha }{108-76}=\frac{\beta }{19-72}=\frac{-1}{16-6}\] \[\therefore \alpha =\frac{-32}{10}=\frac{16}{5}\] \[\beta =\frac{53}{10}\]Thus, centre of the circle, \[\left( \alpha ,\beta  \right)=\left( \frac{-16}{5},\frac{53}{10} \right)\] Hence, option [c]is correct