question_answer

Three lines \[\mathbf{px}+\mathbf{qy}+\mathbf{r}=\mathbf{0};\mathbf{qx}+\mathbf{ry}+\mathbf{p}=\mathbf{0}\]and \[\mathbf{rx}+\mathbf{py}+\mathbf{q}=\mathbf{0}\]are concurrent; If

A) \[p+q+r=pqr\]                   

B) \[{{p}^{2}}+{{q}^{2}}+{{r}^{2}}=pr+rq\]

C) \[{{p}^{3}}+{{q}^{3}}+{{r}^{3}}=3pqr\]                       

D) None of these

Correct Answer: C

Solution :

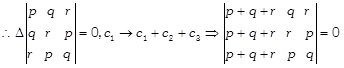
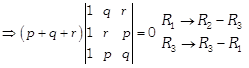
[c] \[\therefore px+qy+r=0\] \[qx+ry+p=0\] \[\And rx+py+q=0\]be concurrent.  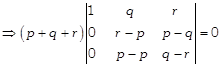                                 \[\Rightarrow \left( p+q+r \right)\left\{ \left( r-p \right)\left( q-r \right)-{{\left( p-q \right)}^{2}} \right\}=0\] \[\Rightarrow \left( p+q+r \right)\left\{ rq-pq-{{r}^{2}}+pr-{{p}^{2}}-{{q}^{2}}+2pq \right\}=0\]\[\Rightarrow (p+q+r)({{p}^{2}}+{{q}^{2}}-{{r}^{2}}-pq-qr-rp)=0\] \[{{p}^{2}}+{{q}^{2}}+{{r}^{2}}=3pqr\]