question_answer

Passage: (Q. - 73) A triangle ABC is inscribed in a circle with AL, BM & CN as the diameters of circumcircle, then If AL, BM & CN are angular bisectors of triangle, then if \[{{\Delta }_{1}}=\]area of \[\Delta ABC\And {{\Delta }_{2}}=Ar.\]of \[\Delta LMN,\]then

A) \[{{\Delta }_{1}}={{\Delta }_{2}}\]                            

B) \[{{\Delta }_{1}}\ge {{\Delta }_{2}}\]

C) \[{{\Delta }_{1}}\le {{\Delta }_{2}}\]                        

D) \[{{\Delta }_{1}}>{{\Delta }_{2}}\]

Correct Answer: C

Solution :

From figure \[\angle ABL=\angle ACL={{90}^{0}}\]\[\angle ALC=\angle ABC=\angle B\](angle in same segment)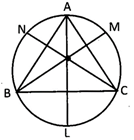 Similarly, \[\angle ALB=\angle ACB=\angle C\] In \[\angle ABL,BL=c\cot \,C\And LC=b\,cot\,B\] \[\therefore \]Area of \[\Delta BLC=\frac{BL.CL.BC}{4R}=\frac{abc}{4R}\cot B.\cot C=2{{r}^{2}}\sin A\cos B\cos C\]Hence, sum of area of \[\Delta 'sBLC,CMA\And ANB\] is \[=2{{R}^{2}}[sinAcosBcosC+sinBcosAcosC\]\[+\sin C\cos A\cos B]\] \[=2{{R}^{2}}\sin A\sin B\sin C=\frac{abc}{4R}={{\Delta }_{1}}\] Also,\[\angle ALN=\angle ACN=\frac{C}{2}\] \[\angle ALM=\angle ABM=\frac{B}{2}\] \[\therefore \]\[\angle NLM=\frac{B+C}{2}={{90}^{0}}-\frac{A}{2}\] \[\therefore \]\[{{\Delta }_{2}}(Ar.of\,\Delta LMC)\] \[=2{{R}^{2}}\sin \left( \frac{\pi }{2}-\frac{A}{2} \right)\sin \left( \frac{\pi }{2}-\frac{B}{2} \right)\sin \left( \frac{\pi }{2}-\frac{C}{2} \right)\] \[=2{{R}^{2}}\cos \frac{A}{2}\cos \frac{B}{2}\cos \frac{C}{2}\] \[\therefore \]\[{{\Delta }_{1}}\le {{\Delta }_{2}}\]