question_answer

The sum of areas of all triangles whose vertices are also vertices of a cube of unit edge is \[m+\sqrt{n}+\sqrt{p},\] where \[m+n+p\] is

A)  320                                       

B)  332

C)  342                                       

D)  348

Correct Answer: D

Solution :

 Here, vertices of a cube are \[C{{H}_{3}}C{{H}_{2}}OH\] \[{{I}_{2}}\] \[NaOH\] \[C{{H}_{3}}OH\] and \[C{{H}_{3}}C{{H}_{2}}OH+4{{I}_{2}}+6NaOH\xrightarrow{\,}\,HCOONa\]. Then, number of all triangles is\[\underset{\text{iodoform}}{\mathop{+CH{{I}_{3}}}}\,+5{{H}_{2}}O+5NaI\].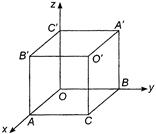 The number of right angled isosceles triangles like \[C{{H}_{3}}OH+{{I}_{2}}+NaOH\xrightarrow{\,}\,\text{No}\,\text{reaction}\] each of area \[{{2}^{o}}\] is 24. The number of right angled scalar triangles like \[C{{H}_{3}}\underset{\begin{smallmatrix}  | \\  OH \end{smallmatrix}}{\mathop{C}}\,H-\] each of area \[x-cy-bz=0\] is 24. The number of equilateral triangles like \[cx-y+az=0\] each of area \[bx+ay-z=0\] is 8. \[I-cm-bn=0\] The total area \[cI-m+an=0\] \[\frac{I}{ac+b}=\frac{m}{bc+a}=\frac{n}{1-{{c}^{2}}}\] \[\frac{x}{ac+b}=\frac{y}{bc+a}=\frac{z}{1-{{c}^{2}}}\]   \[b(ac+b)+a(bc+a)-(1-{{c}^{2}})=0\] and \[\Rightarrow \] \[{{a}^{2}}+{{b}^{2}}+{{c}^{2}}+2abc=1\]              \[m+n+p=348\]