question_answer

If PQ is a double ordinate of hyperbola \[\frac{{{x}^{2}}}{{{a}^{2}}}-\frac{{{y}^{2}}}{{{b}^{2}}}=1\] such that OPQ is an equilateral triangle, O being the centre of the hyperbola. Then the eccentricity e of the hyperbola satisfies

A) \[1<e<2\sqrt{3}\]                  

B)   \[e=2/\sqrt{3}\]

C)   \[e=\sqrt{3}/2\]                      

D)   \[e>2\sqrt{3}\]

Correct Answer: D

Solution :

Let \[\operatorname{P}(a\,\,sec\,\theta ,\,\,b\,\,\tan \,\theta )\] and \[Q\,\left( a\,sec\,\theta ,-\,b\,tan\,\theta  \right)\]be and points of double ordinates and C(0, 0), is the centre of the hyperbola. Now \[PQ=\,\,2b\,\,\tan \,\theta \]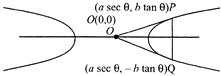 \[\operatorname{OQ}=OP\,\,=\,\,\sqrt{{{a}^{2}}{{\sec }^{2}}\theta +{{b}^{2}}{{\tan }^{2}}\theta }\] Since, OPQ is an equilateral triangle (given) \[\therefore \,\,\,\,OQ=OP=PQ,\] \[\therefore \,\,\,4{{b}^{2}}\,{{\tan }^{2}}\theta  ={{a}^{2}}\,se{{c}^{2}}\theta  +\,\,{{b}^{2}}ta{{n}^{2}}\theta \] \[\Rightarrow \,\,\,3{{b}^{2}}ta{{n}^{2}}\theta ={{a}^{2}}\,se{{c}^{2}}\theta \,\,\Rightarrow \,\,3{{b}^{2}}si{{n}^{2}}\theta ={{a}^{2}}\] \[\Rightarrow \,\,\,3{{a}^{2}}({{e}^{2}}-1)\,si{{n}^{2}}\theta \,\,=\,\,{{a}^{2}},\,\,\,\,\,\,\,\,\,\,\,\,\,\,\left[ \because \,\,e=\sqrt{1-\frac{{{b}^{2}}}{{{a}^{2}}}} \right]\]        \[\Rightarrow \,\,3({{e}^{2}}-1)\,si{{n}^{2}}\theta =1\] \[\Rightarrow \,\,\frac{1}{3({{e}^{2}}-1)}\,=\,\,si{{n}^{2}}\theta <1,\,\,\,\,\,\,(\because \,\,si{{n}^{2}}\,\,\theta <1)\] \[\Rightarrow \,\,\frac{1}{{{e}^{2}}-1}\,<3\,\,\Rightarrow \,\,{{e}^{2}}-1>\frac{1}{3}\Rightarrow {{e}^{2}}>\frac{4}{3}\Rightarrow e>\frac{2}{\sqrt{3}}\]