| If each edge of a cube is doubled |
| (a) How many times will its surface area increase? |
| (b) How many times will its volume increase? |
| Factorise: |
| (a) \[12x+36\] |
| (b) \[22y-33z\] |
| Simplify : \[3x\left( 4x-5 \right)+3\]and find its value |
| (a) \[x=3\] |
| (b) \[x=\frac{1}{2}:\] |
| X | (i) \[{{p}_{1}}\] | 200 | 300 |
| y | 60 | 30 | (ii) \[{{p}_{2}}\] |
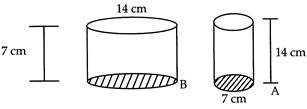
| (a) Construct a rectangle ABCD in which side BC = 5 cm and diagonal BD = 6.2 cm. |
| (b) Can you draw a rhombus ZEAL, where ZE = 3.5 cm, diagonal EL = 5 cm? Why? |
| (a) Find the compound interest on Rs. 31250 at 8% per annum for \[2\frac{3}{4}\] years. |
| (b) Mohit bought a CD for Rs. 750 and sold it for Rs. 875. Show that his gain percent is \[16\frac{2}{3}\]%. |
| (a) Draw the graph of the function y = 3x + 1. |
| (b) The given graph represents the total runs scored by two batsmen A and B, during each of the ten different matches in the year 2014. |
 |
| Study the graph and answer the following questions: |
| (a) What information is given on the two axes? |
| (b) Which line shows the runs scored by batsman A? |
| Factorise: |
| (a) \[{{a}^{4}}-{{b}^{4}}\] |
| (b) \[{{p}^{4}}-81\] |
| (c) \[{{x}^{4}}-{{\left( y+z \right)}^{4~~}}\] |
| (d) \[{{x}^{4}}-{{(x-z)}^{4}}\] |
| (a) Add: \[p\text{ }(p\text{ }-\text{ }q),\text{ }q\text{ }\left( q\text{ }-\text{ }r \right)\]and \[r\text{ }\left( r\text{ }-\text{ }p \right)\] |
| (b) Add: \[2x\left( z-x-y \right)\] and \[2y\left( z-y-x \right)\] |
| (c) Subtract: 31 \[(I-4m+5n)\]from \[4l\left( 10n-3m+2l \right)\] |
| (d) Subtract: \[3a\left( a+\text{b}+c \right)-2b\text{ }\left( a-b+c \right)\] from \[4c\text{ }\left( -a\text{ }+\text{ b }+\text{ }c \right)\] |
You need to login to perform this action.
You will be redirected in
3 sec
