A) \[\text{AB}+\text{BC+CD}=3\times \text{AD}\]
B) \[\angle \text{ABC}+\angle \text{ADC}=\angle \text{BAD+}\angle \text{BCD}\]
C) \[\text{AB}+\text{BC}=\text{AD}+\text{CD}\]
D) \[\angle \text{ABC}+\angle \text{BCD}+\angle \text{ADC}=360{}^\circ \]
E) None of these
Correct Answer: D
Solution :
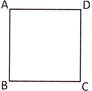
Explanation: Option (d) is correct. Since, ABCD is a square, therefore, \[\angle \text{ABC}=\angle \text{BCD}=\angle \text{ADC}=\angle \text{BAD}=90{}^\circ \](each) And, AB= BC = CD = AD = 1 unit (say) Now, in option (a); AB + BC + CD = (\[1+1+1\]) units = 3 units = \[3\times 1\] unit = \[3\times \text{AD}\] In option (b)\[\angle \text{ABC}+\angle \text{ADC}=90{}^\circ +90{}^\circ =180{}^\circ \]; \[\angle \text{BAD}+\angle \text{BCD}=90{}^\circ +90{}^\circ =180{}^\circ \] In option (c); AB + BC = 1 unit + 1 unit = 2 units; AD + CD = 1 unit + 1 unit = 2 units In option (d); \[\angle \text{ABC}+\angle \text{BCD}+\angle \text{ADC}=\] \[90{}^\circ +90{}^\circ +90{}^\circ =270{}^\circ \] (not \[360{}^\circ \])You need to login to perform this action.
You will be redirected in
3 sec
