-
question_answer1)
A number 'n' is divided by 5 and 4 is added to the result. If the answer is 9, which of the following equations matches the given statements?
A)
\[4=9+\frac{n}{5}\] done
clear
B)
\[\frac{n}{5}+4=9\] done
clear
C)
\[\frac{5}{n}=4\] done
clear
D)
\[\frac{n+4}{5}=9\] done
clear
View Solution play_arrow
-
question_answer2)
A shopkeeper has x kilograms of tea in stock. He sells 15 kilograms and then receives a new shipment weighing 2y kilograms. Which expression represents the weight of the tea he now has?
A)
\[(x-15-2y)\,kg\] done
clear
B)
\[(x+15+2y)\,kg\] done
clear
C)
\[(x+15-2y)\,kg\] done
clear
D)
\[(x-15+2y)\,kg\] done
clear
View Solution play_arrow
-
question_answer3)
If 15 is subtracted from three times a number, the result is 16. Identify the algebraic expression for the statement.
A)
\[x-15=16\] done
clear
B)
\[3x-15=16\] done
clear
C)
\[x+15=16\] done
clear
D)
\[3x+15=16\] done
clear
View Solution play_arrow
-
question_answer4)
Find the algebraic expressions for the following statement.
| \[\frac{{{3}^{th}}}{4}\] of the sum of numbers m and n. |
A)
\[\frac{1}{4}(m\,n)\] done
clear
B)
\[\frac{1}{4}(m\,+\,n)\] done
clear
C)
\[\frac{3}{4}(m\,+\,n)\] done
clear
D)
\[\frac{3}{4}mn\] done
clear
View Solution play_arrow
-
question_answer5)
Ram secured 80 marks in English, x marks in Mathematics and 99 marks in Science. Find her total marks.
A)
\[180+x\] done
clear
B)
\[189+x\] done
clear
C)
\[179+x\] done
clear
D)
\[190+x\] done
clear
View Solution play_arrow
-
question_answer6)
Venu spends Rs. x daily and saves Rs. y per week. What is his income after 4 weeks?
A)
\[Rs.(7x+21y)\] done
clear
B)
\[Rs.(28x+4y)\] done
clear
C)
\[Rs.(4x+28y)\] done
clear
D)
\[Rs.(4y+x)\] done
clear
View Solution play_arrow
-
question_answer7)
A note-book costs \[Rs.15\] and a pencil costs\[Rs.1.5\]. If I have \[Rs.x\] with me, what is the balance after I purchase 12 note-books and 10 pencils?
A)
\[Rs.(x-175)\] done
clear
B)
\[Rs.(x-185)\] done
clear
C)
\[Rs.(x-195)\] done
clear
D)
\[Rs.(x-165)\] done
clear
View Solution play_arrow
-
question_answer8)
Which system of equations represents the following statements?
| The sum of two numbers is ten. One number is five times the other. |
A)
\[\begin{matrix} xy=10 \\ y=5x \\ \end{matrix}\] done
clear
B)
\[\begin{matrix} xy=10 \\ y=x+5 \\ \end{matrix}\] done
clear
C)
\[\begin{matrix} x+y=10 \\ y=5x \\ \end{matrix}\] done
clear
D)
\[\begin{matrix} x+y=10 \\ y=x+5 \\ \end{matrix}\] done
clear
View Solution play_arrow
-
question_answer9)
A rectangular volleyball court has a width of x m and a length of\[2x\text{ }m\]. Which expression gives the area of the court in square metres?
A)
\[3x\] done
clear
B)
\[2{{x}^{2}}\] done
clear
C)
\[3{{x}^{2}}\] done
clear
D)
\[2{{x}^{3}}\] done
clear
View Solution play_arrow
-
question_answer10)
Sunitha's family went on a vacation. They started with \[\text{Rs}.2000.\]If they spent \[\text{Rs}\text{.15}0\] each day, which expression represents how much money they had after x days?
A)
\[\text{Rs}\text{.1850x}\] done
clear
B)
\[\text{Rs}.2000-150x\] done
clear
C)
\[\text{Rs}.150x\] done
clear
D)
\[\text{Rs}.2000+150x\] done
clear
View Solution play_arrow
-
question_answer11)
Anitha had some change with her. After her friend gave her \[Rs.0.45,\] Anitha had \[Rs.1.35,\] altogether. Which equation can housed to find the original amount of money, m, she had at first?
A)
\[Rs.(m\times 0.45)=Rs.1.35\] done
clear
B)
\[Rs.1.35=Rs.(m-0.45)\] done
clear
C)
\[Rs.m=Rs.(1.35-0.45)\] done
clear
D)
\[Rs.(m+1.35)=Rs.0.45\] done
clear
View Solution play_arrow
-
question_answer12)
Which algebraic equation best describes the total growth (T) in height of pine trees over a 3-year period, if g equals the rate of growth in centimetres per year?
A)
\[T=3\times g\] done
clear
B)
\[T=3+g\] done
clear
C)
\[T=\frac{g}{3}\] done
clear
D)
\[T=\frac{3}{8}\] done
clear
View Solution play_arrow
-
question_answer13)
The rectangle shown has length 15 inches and perimeter P inches.
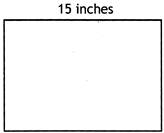
Which equation could be used to find the width of the rectangle?
A)
\[P=15+\frac{w}{2}\] done
clear
B)
\[P-15-w\] done
clear
C)
\[P=30+2w\] done
clear
D)
\[P=30-2w\] done
clear
View Solution play_arrow
-
question_answer14)
A square with a side of \[xm\] is inside a square with a side of \[4\text{ }m,\]as shown in the figure. Which expression represents the area of the shaded region in terms of x?
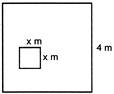
A)
\[(16+{{x}^{2}}){{m}^{2}}\] done
clear
B)
\[(16-{{x}^{2}}){{m}^{2}}\] done
clear
C)
\[(16-2x){{m}^{2}}\] done
clear
D)
\[(16-4x){{m}^{2}}\] done
clear
View Solution play_arrow
-
question_answer15)
What value of 'k' makes the following equation true?
A)
\[108\] done
clear
B)
\[98\] done
clear
C)
\[39\] done
clear
D)
\[12\] done
clear
View Solution play_arrow
-
question_answer16)
If \[t=-\text{ }5,\]find the value of \[3{{t}^{2}}+7t-9\].
A)
\[42\] done
clear
B)
\[31\] done
clear
C)
\[28\] done
clear
D)
\[50\] done
clear
View Solution play_arrow
-
question_answer17)
Find the value of \[{{x}^{2}}+{{y}^{2}}+{{z}^{2}}-xy-zy-zx\] when \[x=-3,\text{ }y=4\]and \[z=-2\].
A)
75 done
clear
B)
68 done
clear
C)
43 done
clear
D)
54 done
clear
View Solution play_arrow
-
question_answer18)
What value of w makes the equation in the box true?
| \[5\times w=(5\times 20)+(5\times 3)\] |
A)
3 done
clear
B)
20 done
clear
C)
23 done
clear
D)
203 done
clear
View Solution play_arrow
-
question_answer19)
Vinay a charges \[Rs.15\]per hour to baby-sit. Which equation could she use to find the number of hours (h) she needs to baby-sit in order to earn \[Rs.150\]?
A)
\[15h=150\] done
clear
B)
\[\frac{h}{15}=150\] done
clear
C)
\[h-15=150\] done
clear
D)
\[15+h=150\] done
clear
View Solution play_arrow
-
question_answer20)
Which equation shows the relationship satisfied by all the values in the given table?
| x | y |
| \[-2\] | \[-6\] |
| \[-1\] | \[-3\] |
| \[0\] | \[0\] |
| \[1\] | \[3\] |
| \[2\] | \[6\] |
A)
\[y=3x\] done
clear
B)
\[x=y+3\] done
clear
C)
\[y=x+3\] done
clear
D)
\[x=3y\] done
clear
View Solution play_arrow
-
question_answer21)
What value of 'x' makes the given equation true?
A)
2 done
clear
B)
18 done
clear
C)
66 done
clear
D)
126 done
clear
View Solution play_arrow
-
question_answer22)
Find the solution of\[-3x+2=-7\].
A)
\[x=-6\] done
clear
B)
\[x=-3\] done
clear
C)
\[x=3\] done
clear
D)
\[x=6\] done
clear
View Solution play_arrow
-
question_answer23)
Latha needs \[\text{Rs}\text{.6}0\]for a class trip. She has \[\text{Rs}\text{.32}\]. She can earn \[\text{Rs}\text{.4}\]an hour working part time. If the equation given shows this relationship, how many hours must Latha work to have the money she needs?
A)
7 hours done
clear
B)
17 hours done
clear
C)
23 hours done
clear
D)
28 hours done
clear
View Solution play_arrow
-
question_answer24)
What value of 'x' satisfies the equation \[4x+2=22?\]
A)
\[3.5\] done
clear
B)
\[5.0\] done
clear
C)
\[6.0\] done
clear
D)
\[7.5\] done
clear
View Solution play_arrow
-
question_answer25)
Which expression is the result of applying the distributive property to \[8\times (100+5)?\]?
A)
\[8\times 105\] done
clear
B)
\[8\times 140\] done
clear
C)
\[800+5\] done
clear
D)
\[800+40\] done
clear
View Solution play_arrow
-
question_answer26)
If \[a=8,\text{ }b=2\]and \[c=3,\]find the value of \[\frac{16bc-5ab}{abc-3{{b}^{2}}}\].
A)
\[\frac{2}{3}\] done
clear
B)
\[\frac{1}{6}\] done
clear
C)
\[\frac{4}{9}\] done
clear
D)
\[\frac{3}{8}\] done
clear
View Solution play_arrow
-
question_answer27)
Which property is used in the equation given?
A)
Associative Property of Addition done
clear
B)
Commutative Property of Addition done
clear
C)
Distributive Property done
clear
D)
Reflexive Property done
clear
View Solution play_arrow
-
question_answer28)
A telephone company charges \[Rs.0.05\]per minute for local calls and \[\text{Rs}.0.12\]per minute for long distance calls. Which expression gives the total cost in rupees for "x" minutes of local calls and "y" minutes of long-distance calls?
A)
\[Rs.(0.05x+0.12y)\] done
clear
B)
\[Rs.(0.05x-0.12y)\] done
clear
C)
\[Rs.(0.17(x+y))\] done
clear
D)
\[Rs.0.17xy\] done
clear
View Solution play_arrow
-
question_answer29)
A fruit-seller bought W apples at \[Rs.30\] each and 'n' mangoes at \[Rs.55\]each. He sold the apples at \[Rs.50\] each and the mangoes at \[Rs.70\] each. Identify the expression for his total profit.
A)
\[Rs.(10m+12m)\] done
clear
B)
\[Rs.(16m+17n)\] done
clear
C)
\[Rs.(12m-16n)\] done
clear
D)
\[Rs.(20m+15n)\] done
clear
View Solution play_arrow
-
question_answer30)
An adult ticket costs Rs. x and a child ticket cost Rs. y. Ramani buys 3 adult tickets and 5 child tickets. If she pays with a Rs. 50 note, find the change that she gets.
A)
\[Rs.(50+3x+y)\] done
clear
B)
\[Rs.(50-3x-5y)\] done
clear
C)
\[Rs.(50-x+y)\] done
clear
D)
\[Rs.(50+5x-3y)\] done
clear
View Solution play_arrow
-
question_answer31)
Find the algebraic expression for the difference of 7 and product of p and q.
A)
\[pq-7\] done
clear
B)
\[7+pq\] done
clear
C)
\[7-pq\] done
clear
D)
\[7p-q\] done
clear
View Solution play_arrow
-
question_answer32)
If \[h=3\]and \[k=4,\]find the value of \[\frac{hk+4}{2}-2\].
A)
6 done
clear
B)
7 done
clear
C)
8 done
clear
D)
10 done
clear
View Solution play_arrow
-
question_answer33)
Find the value of \[({{x}^{4}}+{{y}^{2}})\div (a+b)\] when \[x=y=a=b=3\].
A)
15 done
clear
B)
12 done
clear
C)
6 done
clear
D)
3 done
clear
View Solution play_arrow
-
question_answer34)
Lila obtained 8 marks in a Science test. Her friend, Maria, obtained x marks more than her. How many marks did they get altogether?
A)
\[2x\] done
clear
B)
\[2x+8\] done
clear
C)
\[16+x\] done
clear
D)
\[16+2x\] done
clear
View Solution play_arrow
-
question_answer35)
What is the value of \[(3+{{5}^{2}})\div 4-(x+1)\] when \[x=7\] 7?
A)
\[-7\] done
clear
B)
\[-1\] done
clear
C)
\[8\] done
clear
D)
\[10\] done
clear
View Solution play_arrow
-
question_answer36)
Mr. A is now \[(x-10)\] years old. How old will he be 10 years from now?
A)
\[(x-20)\] years done
clear
B)
\[(x+10)\] years done
clear
C)
x years done
clear
D)
\[x+20\] years done
clear
View Solution play_arrow
-
question_answer37)
Find the algebraic expression for the statement: "Product of x and a subtracted from the product of b and y'.
A)
\[ax-by\] done
clear
B)
\[x+a-by\] done
clear
C)
\[by-ax\] done
clear
D)
\[xa-b-y\] done
clear
View Solution play_arrow
-
question_answer38)
In a train there were \[9x+12y\]people. At three successive stations, \[3x,\text{ }4y\]and \[2x\]people got down. How many people were left in the train?
A)
\[4x+8y\] done
clear
B)
\[4y+8x\] done
clear
C)
\[4x-8y\] done
clear
D)
\[8y-4x\] done
clear
View Solution play_arrow
-
question_answer39)
If \[2=x,(-3)=y\] and \[5=z,\] find the value of \[4\times (2)\times {{(-3)}^{2}}-15{{(2)}^{2}}(-3)+(2)\times (5)\].
A)
\[4x{{y}^{2}}-15{{x}^{2}}y-zx\] done
clear
B)
\[4x{{y}^{2}}-15{{x}^{2}}y+zx\] done
clear
C)
\[4x{{y}^{2}}+15{{x}^{2}}y+zx\] done
clear
D)
\[4{{x}^{2}}y+15y{{x}^{2}}+zx\] done
clear
View Solution play_arrow
-
question_answer40)
Which situation could be described by the given expression?
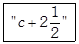
A)
Lata jogged "c" kilometres yesterday and then \[2\frac{1}{2}\]. Kilometres farther today. done
clear
B)
Lata jogged "c" yesterday kilometres and \[2\frac{1}{2}\]. Kilometres fewer today. done
clear
C)
Lata jogged \[2\frac{1}{2}\]. yesterday kilometres and "c" kilometres fewer today. done
clear
D)
Lata jogged \[2\frac{1}{2}\]. yesterday kilometres and "c" times as far today. done
clear
View Solution play_arrow
![]()
